题目内容
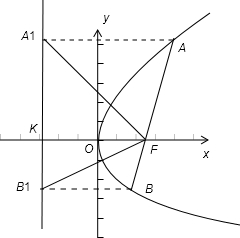
已知抛物线方程为y2=2px(p>0),过焦点F的直线l与抛物线交于A(x1,y1)、B(x2,y2),AA1、BB1垂直于准线,垂足分别为A1、B1,AB的中垂线交x轴于点R.求证:
(1)x1x2=
,y1y2=-p2;
(2)通径长为2p,且通径是最短的焦点弦;
(3)以AB为直径的圆与准线相切;
(4)∠A1FB1=90°;
(5)
+
=
;
(6)|FR|=
.
(1)x1x2=
| p2 |
| 4 |
(2)通径长为2p,且通径是最短的焦点弦;
(3)以AB为直径的圆与准线相切;
(4)∠A1FB1=90°;
(5)
| 1 |
| |AF| |
| 1 |
| |BF| |
| 2 |
| p |
(6)|FR|=
| |AB| |
| 2 |
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设直线方程为x=my+
,代入y2=2px,可得y2-2mpy+p2=0,利用韦达定理,x1•x2=
•
=
,可得结论;
(2)根据通径的概念,可得结论;
(3)PQ的中点是M且到准线的距离是d.设P到准线的距离d1=|PF|,Q到准线的距离d2=|QF|.结合中位线的定义与抛物线的定义可得:
=
=半径,进而得到答案.
(4)由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,可得答案.
(5)AB倾斜角为α,则
+
=
+
=
;
(6)设A1B1的中点为O1,连接O1F,证明|FR|=
,只要证明O1F⊥AB.
| p |
| 2 |
| y12 |
| 2p |
| y22 |
| 2p |
| p2 |
| 4 |
(2)根据通径的概念,可得结论;
(3)PQ的中点是M且到准线的距离是d.设P到准线的距离d1=|PF|,Q到准线的距离d2=|QF|.结合中位线的定义与抛物线的定义可得:
| |AF|+|BF| |
| 2 |
| |AB| |
| 2 |
(4)由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,可得答案.
(5)AB倾斜角为α,则
| 1 |
| |AF| |
| 1 |
| |BF| |
| 1-cosα |
| p |
| 1+cosα |
| p |
| 2 |
| p |
(6)设A1B1的中点为O1,连接O1F,证明|FR|=
| |AB| |
| 2 |
解答:
 解:(1)设直线方程为x=my+
解:(1)设直线方程为x=my+
,代入y2=2px,可得y2-2mpy+p2=0,
∴y1y2=-p2,x1•x2=
•
=
;
(2)根据通径的概念,令x=
,可得y=±p,∴通径长为2p,且通径是最短的焦点弦;
(3)由于过焦点的弦为AB,AB的中点是M,M到准线的距离是d.
而A到准线的距离d1=|AF|,Q到准线的距离d2=|BF|.
又M到准线的距离d是梯形的中位线,故有d=
,
由抛物线的定义可得:
=
,等于半径.
所以圆心M到准线的距离等于半径,所以圆与准线是相切.
(4)如图:设准线与x轴的交点为K,∵A、B在抛物线的准线上的射影为A1、B1,
由抛物线的定义可得,AA1=AF,∴∠AA1F=∠AFA1,又由内错角相等得∠AA1F=∠A1FK,∴∠AFA1=∠A1FK.
同理可证∠BFB1=∠B1 FK.
由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,
∴∠A1FK+∠B1FK=∠A1FB1=90°,
(5)AB倾斜角为α,则
+
=
+
=
;
(6)设A1B1的中点为O1,连接O1F,则
因为AB的中垂线交x轴于点R,
所以要证明|FR|=
,只要证明O1F⊥AB.O1(-
,
),F(
,0),
∴kO1F=-
,
设直线方程为x=my+
,代入y2=2px,可得y2-2mpy+p2=0,
∴y1+y2=2mp,
∴kO1F=-
=-m,
∴O1F⊥AB,
∴MO1FR是平行四边形
∴|FR|=MO1=
.
 解:(1)设直线方程为x=my+
解:(1)设直线方程为x=my+| p |
| 2 |
∴y1y2=-p2,x1•x2=
| y12 |
| 2p |
| y22 |
| 2p |
| p2 |
| 4 |
(2)根据通径的概念,令x=
| p |
| 2 |
(3)由于过焦点的弦为AB,AB的中点是M,M到准线的距离是d.
而A到准线的距离d1=|AF|,Q到准线的距离d2=|BF|.
又M到准线的距离d是梯形的中位线,故有d=
| |AF|+|BF| |
| 2 |
由抛物线的定义可得:
| |AF|+|BF| |
| 2 |
| |AB| |
| 2 |
所以圆心M到准线的距离等于半径,所以圆与准线是相切.
(4)如图:设准线与x轴的交点为K,∵A、B在抛物线的准线上的射影为A1、B1,
由抛物线的定义可得,AA1=AF,∴∠AA1F=∠AFA1,又由内错角相等得∠AA1F=∠A1FK,∴∠AFA1=∠A1FK.
同理可证∠BFB1=∠B1 FK.
由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,
∴∠A1FK+∠B1FK=∠A1FB1=90°,
(5)AB倾斜角为α,则
| 1 |
| |AF| |
| 1 |
| |BF| |
| 1-cosα |
| p |
| 1+cosα |
| p |
| 2 |
| p |
(6)设A1B1的中点为O1,连接O1F,则
因为AB的中垂线交x轴于点R,
所以要证明|FR|=
| |AB| |
| 2 |
| p |
| 2 |
| y1+y2 |
| 2 |
| p |
| 2 |
∴kO1F=-
| y1+y2 |
| 2p |
设直线方程为x=my+
| p |
| 2 |
∴y1+y2=2mp,
∴kO1F=-
| y1+y2 |
| 2p |
∴O1F⊥AB,
∴MO1FR是平行四边形
∴|FR|=MO1=
| |AB| |
| 2 |
点评:本题主要考查抛物线的性质应用,解决此类问题的关键是熟练掌握抛物线的定义,以及直线与圆的位置关系的判定,属于中档题.

练习册系列答案
相关题目
己知函数f(x)=lnx-
,则函数f(x)的零点所在的区间是( )
| x |
| 4 |
| A、.(0,1) |
| B、(1,2) |
| C、.(2,3) |
| D、(3,4) |
设α表示平面,a,b表示两条不同的直线,给定下列四个命题:
①a∥α,a⊥b⇒b⊥α;②a∥b,a⊥α⇒b⊥α;③a⊥α,a⊥b⇒b∥α;④a⊥α,b⊥α⇒a∥b.
其中正确的是( )
①a∥α,a⊥b⇒b⊥α;②a∥b,a⊥α⇒b⊥α;③a⊥α,a⊥b⇒b∥α;④a⊥α,b⊥α⇒a∥b.
其中正确的是( )
| A、①② | B、②④ | C、③④ | D、②③ |
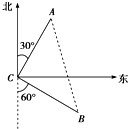 两灯塔A、B与海洋观察站C的距离都等于2
两灯塔A、B与海洋观察站C的距离都等于2| 2 |
| A、2 km |
| B、3 km |
| C、4 km |
| D、5 km |