题目内容

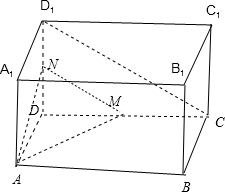
已知长方体ABCD-A1B1C1D1中，侧面A1ADD1是正方形，M是棱CD的中点，AM与CD1所成角为θ，若sinθ=
78
9
，则
AA1
AB
的值为（　　）
A、
2
B、
2
2
3
C、
2
2
D、
3
2
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：取DD1中点N，连MN，AN，AM与CD1所成的角就是AM与MN所成角，mh AM与CD1所成角为θ，sinθ=
78
9
，得cosθ=
3
9
，设AA1=AD=2a，AB=2b，由余弦定理，能求出
AA1
AB
的值．
解答： 解：取DD1中点N，连MN，AN，
∵MN平行CD1，∴AM与CD1所成的角就是AM与MN所成角，
∵AM与CD1所成角为θ，sinθ=
78
9
，∴cosθ=
3
9
，
设AA1=AD=2a，AB=2b
则MN=
a2+b2
，AN=
5a
，AM=
4a2+b2
，
由余弦定理，得：
cos∠AMN=
4a2+b2+a2+b2-5a2
2
a2+b2
•
4a2+b2
=
3
a
9
，
3
3
•b2=
a2+b2
•
4a2+b2
，
两边平方，得：
27b4=4a4+5a2b2+b4，
（a2-2b2）（4a2+13b2）=0，
a2=2b2，
a=
2
b
∴
AA1
AB
=
a
b
=
2
．
点评：本题考查两线段比值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
若关于x的方程x2+（m-3）x+m=0有两个不同的实根x1，x2，且满足x1＞1，x2＜1，求m的取值范围．
已知定点A（0，-3），动点P在x轴上移动，动点Q在y轴上，且∠APQ=
π
2
，点R在直线PQ上且满足
PQ
=
1
2
QR
．
（1）当点P在x轴上移动时，求动点R的轨迹C的方程；
（2）倾斜角为
π
4
的直线l0与轨迹C相切，求切线l0的方程；
（3）已知切线l0与y轴的交点为B，过点B的直线l与轨迹C交于M、N两点，点D（0，1）．若∠MDN为钝角，求直线l的斜率k的取值范围．
设关于x的一元二次方程x2-2ax+b2=0．
（1）若a是从0、1、2、3四个数中任取的一个数，b是从0、1、2三个数中任取的一个数，求上述方程有实根的概率．
（2）若a是从区间[0，3]内任取的一个数，b是从区间[0，2]内任取的一个数，求上述方程有实根的概率．
等边三角形ABC的边长为1，BC边上的高是AD，若沿高AD将它折成一个直二面角B-AD-C，则A到BC的距离是
 
．
设椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2，P是C上的点，PF2⊥F1F2，∠PF1F2=60°，则C的离心率为（　　）
A、
3
6
B、
3
-1
C、
3
2
D、2-
3
已知二次函数y=x2-2ax+5（a为常数）．
（1）如果函数图象的对称轴为x=3，求实数a的值并做出函数的图象；
（2）求此函数在x∈[0，2]上的最小值；
（3）当x∈[0，2]时，此函数恒小于6，求实数a的取值范围．
已知曲线C1的参数方程为
x=-
3
t
y=2
3
+t
（t为参数），曲线C2的极坐标方程为ρ=2，则曲线C2与曲线C1交点个数为
 
．
已知抛物线方程为y2=2px（p＞0），过焦点F的直线l与抛物线交于A（x1，y1）、B（x2，y2），AA1、BB1垂直于准线，垂足分别为A1、B1，AB的中垂线交x轴于点R．求证：
（1）x1x2=
p2
4
，y1y2=-p2；         
（2）通径长为2p，且通径是最短的焦点弦；
（3）以AB为直径的圆与准线相切；    
（4）∠A1FB1=90°；
（5）
1
|AF|
+
1
|BF|
=
2
p
；              
（6）|FR|=
|AB|
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网