题目内容

已知向量
a
=（1，2），
b
=（-3，4）．
（Ⅰ）求
a
+
b
与
a
-
b
的夹角；
（Ⅱ）若
a
⊥（
a
+λ
b
），求实数λ的值．
考点：平面向量数量积的运算,平面向量的坐标运算
专题：平面向量及应用
分析：（I）利用向量的夹角公式即可得出；
（II）利用向量垂直与数量积的关系即可得出．
解答： 解：（Ⅰ）∵向量
a
=（1，2），
b
=（-3，4），
∴
a
+
b
=（-2，6），
a
-
b
=（4，-2），
∴(
a
+
b
)•(
a
-
b
)=-8-12=-20，
∴cos＜
a
+
b
，
a
-
b
＞=
(
a
+
b
)•(
a
-
b
)
|
a
+
b
| |
a
-
b
|
=
-20
40
•
20
=-
2
2
，
∴
a
+
b
与
a
-
b
的夹角为
3π
4
．
（Ⅱ）∵
a
⊥（
a
+λ
b
），∴
a
•(
a
+λ
b
)=0，
∴（1，2）•（1-3λ，2+4λ）=0，
化为1-3λ+4+8λ=0，解得λ=-1．
点评：本题考查了向量的夹角公式、向量垂直与数量积的关系，属于基础题．
练习册系列答案
相关题目
若正数项数列{an}的前n项和为Sn，且满足
Sn+1
=
Sn
+1，其中首项a1=1．
（1）求a2，a3及数列{an}的通项公式an；
（2）设bn=
1
an•an+1
，Tn表示数列{bn}的前项和，若对任意的n∈N*，不等式λTn＜n+8×（-1）n恒成立，求实数λ的取值范围．
已知椭圆P的中心O在坐标原点，焦点在x轴上，且经过点A（0，2
3
），离心率为
1
2
．
（Ⅰ）求椭圆P的方程；
（Ⅱ）是否存在过点E（0，-4）的直线l交椭圆P于点R、T，且满足
OR
•
OT
=8，若存在，求直线l的方程；若不存在，说明理由．
已知数列{an}中，a1=1，a2=0，其前n项和Sn满足：Sn+Sn-2=2Sn-1+2n-1-3（n≥3）
（1）试求数列{an}的通项公式；
（2）求数列{an}的前n项和Sn．
已知直线l过两直线x-2y+4=0和x+y-2=0的交点P，求解下列问题：
（1）直线l经过点Q（2，1），求直线l的方程；
（2）直线l与直线3x-4y+5=0平行，求直线l的方程．
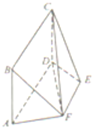如图，几何体ABCDEF中，四边形ABCD为矩形，且平面ABCD⊥平面ADEF，四边形ADEF为等腰梯形，AD∥EF，AD=2，AB=AF=1，∠DAF=60°．
（Ⅰ）证明：AF⊥平面CDF；
（Ⅱ）求几何体ABCDEF的体积．
已知在△ABC中，
a3+b3-c3
a+b-c
=c2，sinA•sinB=
3
4
，则△ABC一定是
 
．
给出定义：若n-0.5＜x≤n+0.5（其中n为整数），则n叫做实数x的“友好整数”，记作{x}，即{x}=n，在此基础上给出下列关于函数f（x）=x-{x}的四个命题；
①f（2.4）=-0.6；
②f（-
1
2
）＞f（
1
3
）；
③f（-
1
4
）×f（
1
4
）=f（-
1
16
）；
④y=f（x）的定义域为R，值域是[-
1
2
，
1
2
]；
则其中真命题的序号是
 
．
已知关于x的不等式x+
1
x-a
≥5在x∈（a，+∞）上恒成立，则实数a的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网