题目内容
数列{an}中,an<0,前n项和Sn=-
(an-1)2.
(1)求数列{an}的通项公式;
(2)设bn=
(n∈N+),Tn=b1+b2+…+bn,若对任意n∈N+,总存在m∈[-1,1]使Tn<m2-2m+t+
成立,求出t的取值范围.
| 1 |
| 4 |
(1)求数列{an}的通项公式;
(2)设bn=
| 1 |
| n(3-an) |
| 1 |
| 2 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:本题(1)将和式转化不项式,研究数列的通项公式,注意要分类讨论;
(2)先通过裂项法求和,再研究能成立问题,求出关于m的函数的最大值,得到本题结论.
(2)先通过裂项法求和,再研究能成立问题,求出关于m的函数的最大值,得到本题结论.
解答:
解:(1)当n=1时,
∵S1=-
(a1-1)2=a1,
∴a1=-1.
当n≥2时,
an=Sn-Sn-1=-
(an-1)2+
(an-1-1)2,
∴4an=-
+2an-1+
-2an-1+1.
∴an-an-1=-2(n≥2).
∴数列{an}是等差数列,
∴an=-2n+1.
(2)∵bn=
=
=
(
-
).
∴Tn=
(1-
)+
(
-
)+…+
(
-
).
=
-
.
∴Tn<
.
设f(m)=m2-2m+t+
,
函数f(m)在m∈[-1,1]内的最大值为t+
,
∴t+
≥
,
∴t≥-3.
∵S1=-
| 1 |
| 4 |
∴a1=-1.
当n≥2时,
an=Sn-Sn-1=-
| 1 |
| 4 |
| 1 |
| 4 |
∴4an=-
| a | 2 n |
| a | 2 n-1 |
∴an-an-1=-2(n≥2).
∴数列{an}是等差数列,
∴an=-2n+1.
(2)∵bn=
| 1 |
| n(3-a n) |
| 1 |
| 2n(n+1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+2 |
∴Tn<
| 1 |
| 2 |
设f(m)=m2-2m+t+
| 1 |
| 2 |
函数f(m)在m∈[-1,1]内的最大值为t+
| 7 |
| 2 |
∴t+
| 7 |
| 2 |
| 1 |
| 2 |
∴t≥-3.
点评:本题考查了数列前n项和与通项公式的关系、裂项法求和、能成立问题,本题难度适中,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
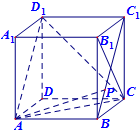 如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列命题:
如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列命题:①AP⊥B1C;
②BP与CD1所成的角是60°;
③VP-AD1C为定值;
④B1P∥平面D1AC;
⑤二面角P-AB-C的平面角为45°.
其中正确命题的个数有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
已知各项均为正数的等差数列{an}的前20项和为100,那么a2•a19的最大值是( )
| A、50 | ||
| B、25 | ||
| C、100 | ||
D、4
|
 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,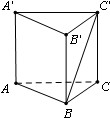 如图,在三棱柱ABC-A′B′C′中,底面ABC是正三角形,AA′⊥底面ABC,且AB=1,AA′=2,则直线BC′与平面ABB′A′所成角的正弦值为
如图,在三棱柱ABC-A′B′C′中,底面ABC是正三角形,AA′⊥底面ABC,且AB=1,AA′=2,则直线BC′与平面ABB′A′所成角的正弦值为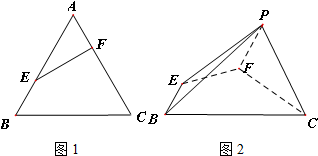 在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC=
在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC=