题目内容
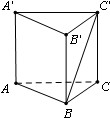 如图,在三棱柱ABC-A′B′C′中,底面ABC是正三角形,AA′⊥底面ABC,且AB=1,AA′=2,则直线BC′与平面ABB′A′所成角的正弦值为
如图,在三棱柱ABC-A′B′C′中,底面ABC是正三角形,AA′⊥底面ABC,且AB=1,AA′=2,则直线BC′与平面ABB′A′所成角的正弦值为考点:直线与平面所成的角
专题:空间角
分析:如图所示,取A′B′的中点D,连接C′D′,BD.利用等边三角形的性质及AA′⊥底面ABC,可得C′D⊥侧面ABB′A′,
于是∠C′BD是直线BC′与平面ABB′A′所成角.利用勾股定理、直角三角形的边角关系即可得出.
于是∠C′BD是直线BC′与平面ABB′A′所成角.利用勾股定理、直角三角形的边角关系即可得出.
解答:
解:如图所示,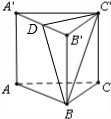
取A′B′的中点D,连接C′D′,BD.
∵底面△A′B′C′是正三角形,
∴C′D⊥A′B′.
∵AA′⊥底面ABC,∴A′A⊥C′D.
又AA′∩A′B′=A′,
∴C′D⊥侧面ABB′A′,
∴∠C′BD是直线BC′与平面ABB′A′所成角.
∵等边△A′B′C′的边长为1,C′D=
.
在Rt△BB′C′中,BC′=
=
.
∴直线BC′与平面ABB′A′所成角的正弦值=
=
.
故答案为:
.

取A′B′的中点D,连接C′D′,BD.
∵底面△A′B′C′是正三角形,
∴C′D⊥A′B′.
∵AA′⊥底面ABC,∴A′A⊥C′D.
又AA′∩A′B′=A′,
∴C′D⊥侧面ABB′A′,
∴∠C′BD是直线BC′与平面ABB′A′所成角.
∵等边△A′B′C′的边长为1,C′D=
| ||
| 2 |
在Rt△BB′C′中,BC′=
| B′B2+B′C′2 |
| 5 |
∴直线BC′与平面ABB′A′所成角的正弦值=
| C′D |
| BC′ |
| ||
| 10 |
故答案为:
| ||
| 10 |
点评:本题考查了线面垂直的判定与性质定理、等边三角形的性质、线面角、勾股定理、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
 为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是( )
为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是( )| A、中位数为83 |
| B、众数为85 |
| C、平均数为85 |
| D、方差为19 |
已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若m∥n,m⊥α,n?β,则α⊥β |
| C、若m∥α,m∥β,则α∥β |
| D、若m∥α,α⊥β,则m⊥β |
下列结论中是错误命题的是( )
| A、命题p:“?x∈R,x2-2≥0”的否定形式为¬p:“?x∈R,x2-2<0” | ||||
| B、若¬p是q的必要条件,则p是¬q的充分条件 | ||||
C、“M>N”是“(
|
函数f(x)=
的图象关于原点对称,g(x)=lg(10x+1)+bx是偶函数,则a+b=( )
| 9x-a |
| 3x |
| A、1 | ||
| B、-1 | ||
C、-
| ||
D、
|