题目内容
 如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的表面积为( )
如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的表面积为( )A、6+4
| ||||
B、8+4
| ||||
C、6+6
| ||||
D、6+2
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:直观图如图所示四棱锥P-ABCD,利用表面积计算公式即可得出.
解答:
解:直观图如图所示四棱锥P-ABCD.
 S△PAB=S△PAD=S△PDC=
S△PAB=S△PAD=S△PDC=
×2×2=2,
S△PBC=
×2
×2
×sin600=2
,
S四边形ABCD=2
×2=4
,
故此棱锥的表面积为6+4
+2
.
故选:A.
 S△PAB=S△PAD=S△PDC=
S△PAB=S△PAD=S△PDC=| 1 |
| 2 |
S△PBC=
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
S四边形ABCD=2
| 2 |
| 2 |
故此棱锥的表面积为6+4
| 2 |
| 3 |
故选:A.
点评:本题考查了四棱锥的三视图及其表面积计算公式,属于基础题.

练习册系列答案
相关题目
下列函数中,与函数f(x)=ln(x+1)有相同定义域的是( )
A、y=
| ||||
B、y=
| ||||
| C、y=|x+1| | ||||
D、y=
|
已知函数f(x)=
+xlnx,则曲线y=f(x)在x=1处的切线方程为( )
| 2 |
| x |
| A、x-y-3=0 |
| B、x-y+3=0 |
| C、x+y-3=0 |
| D、x+y+3=0 |
若过点P(-2
,-2)的直线与圆x2+y2=4有公共点,则该直线的倾斜角的取值范围是( )
| 3 |
A、(0,
| ||
B、[0,
| ||
C、[0,
| ||
D、(0,
|
 如图,A,B分别是椭圆C:
如图,A,B分别是椭圆C: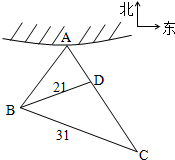 如图所示,近日我渔船编队在岛A周围海域作业,在岛A的南偏西20°方向有一个海面观测站B,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与B相距31海里的C处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛A直线航行以保护我渔船编队,30分钟后到达D处,此时观测站测得B,D间的距离为21海里.
如图所示,近日我渔船编队在岛A周围海域作业,在岛A的南偏西20°方向有一个海面观测站B,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与B相距31海里的C处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛A直线航行以保护我渔船编队,30分钟后到达D处,此时观测站测得B,D间的距离为21海里.