题目内容
已知f(x)=
,在x=x0处取得极值.
(1)证明:f(x0)=-x0;
(2)是否存在实数a,使得对任意x∈(0,+∞),f(x)≥
?若存在,求a的所有值;若不存在,说明理由.
| xlnx |
| 1+x |
(1)证明:f(x0)=-x0;
(2)是否存在实数a,使得对任意x∈(0,+∞),f(x)≥
| a(x-1) |
| x |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)f′(x)=
+
,(x>0).由于函数f(x)=
,在x=x0处取得极值.可得f′(x0)=
+
=0,化简即可证明f(x0)=-x0.
(2)假设存在实数a,使得对任意x∈(0,+∞),f(x)≥
?x2lnx-a(x2-1)≥0恒成立,x∈(0,+∞).令g(x)=x2lnx-a(x2-1),
g′(x)=2xlnx+x-2ax=x(2lnx+1-2a),对a分类讨论:当a=
时,当a>
时,当a<
时,利用导数研究函数的单调性极值与最值即可得出.
| lnx |
| (x+1)2 |
| 1 |
| x+1 |
| xlnx |
| 1+x |
| lnx0 |
| (x0+1)2 |
| 1 |
| x0+1 |
(2)假设存在实数a,使得对任意x∈(0,+∞),f(x)≥
| a(x-1) |
| x |
g′(x)=2xlnx+x-2ax=x(2lnx+1-2a),对a分类讨论:当a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
(1)证明:f′(x)=
+
,(x>0).
∵函数f(x)=
,在x=x0处取得极值.
∴f′(x0)=
+
=0,
∴(1+x0)+lnx0=0,
∴f(x0)+x0=
+x0=
=0,
∴f(x0)=-x0.
(2)解:假设存在实数a,使得对任意x∈(0,+∞),f(x)≥
?x2lnx-a(x2-1)≥0恒成立,x∈(0,+∞).
令g(x)=x2lnx-a(x2-1),
g′(x)=2xlnx+x-2ax=x(2lnx+1-2a),
①当a=
时,g′(x)=2xlnx,
令g′(x)>0,解得x>1,此时函数g(x)单调递增;令g′(x)<0,解得0<x<1,此时函数g(x)单调递减.
∴当x=1时,函数g(x)取得极小值即最小值,g(1)=0,满足g(x)min≥0的条件,因此a=
.
②当a>
时,令g′(x)=0,解得x0=e
>1,可得x∈(x0,+∞),g′(x)>0,函数g(x)单调递增;x∈(0,x0),g′(x)<0,函数g(x)单调递减.
∴g(x0)<g(1)=0,不满足g(x)min≥0的条件,舍去.
③当a<
时,1-2a>0,令g′(x)=0,解得x0=e
<1,可得x∈(x0,+∞),g′(x)>0,函数g(x)单调递增;x∈(0,x0),g′(x)<0,函数g(x)单调递减.
∴g(x0)<g(1)=0,不满足g(x)min≥0的条件,舍去.
综上可得:a=
.
| lnx |
| (x+1)2 |
| 1 |
| x+1 |
∵函数f(x)=
| xlnx |
| 1+x |
∴f′(x0)=
| lnx0 |
| (x0+1)2 |
| 1 |
| x0+1 |
∴(1+x0)+lnx0=0,
∴f(x0)+x0=
| x0lnx0 |
| 1+x0 |
| x0(1+x0+lnx0) |
| 1+x0 |
∴f(x0)=-x0.
(2)解:假设存在实数a,使得对任意x∈(0,+∞),f(x)≥
| a(x-1) |
| x |
令g(x)=x2lnx-a(x2-1),
g′(x)=2xlnx+x-2ax=x(2lnx+1-2a),
①当a=
| 1 |
| 2 |
令g′(x)>0,解得x>1,此时函数g(x)单调递增;令g′(x)<0,解得0<x<1,此时函数g(x)单调递减.
∴当x=1时,函数g(x)取得极小值即最小值,g(1)=0,满足g(x)min≥0的条件,因此a=
| 1 |
| 2 |
②当a>
| 1 |
| 2 |
| 2a-1 |
| 2 |
∴g(x0)<g(1)=0,不满足g(x)min≥0的条件,舍去.
③当a<
| 1 |
| 2 |
| 2a-1 |
| 2 |
∴g(x0)<g(1)=0,不满足g(x)min≥0的条件,舍去.
综上可得:a=
| 1 |
| 2 |
点评:本题考查了利用导数研究函数的单调性极值与最值、恒成立问题的等价转化方法,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
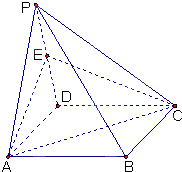 如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且CD⊥面PAD,E 为侧棱PD的中点.
如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且CD⊥面PAD,E 为侧棱PD的中点.