题目内容
3.已知极坐标系的极点与直角坐标系的坐标原点重合、极轴与x轴的正半轴重合,若直线l的极坐标方程为ρsin(θ-$\frac{π}{6}$)=$\frac{\sqrt{3}-1}{2}$.(1)写出直线l的参数方程;
(2)设直线l与圆ρ=2相交于A,B两点,求点P(1,1)到A,B两点的距离之积.
分析 (1)根据直线l的极坐标方程,求出直线的参数方程.
(2)设A,B对应的参数为t1和t2,以直线l的参数方程代入圆的方程整理得到t2+(-3-$\frac{2\sqrt{3}}{3}$)t+$\frac{13}{3}$=0,由|PA|•|PB|=|t1t2|求出点P到A、B两点的距离之积.
解答 解:(1)直线l的极坐标方程为ρsin(θ-$\frac{π}{6}$)=$\frac{\sqrt{3}-1}{2}$,直角坐标方程为y=$\frac{\sqrt{3}}{3}$x+1-$\frac{2\sqrt{3}}{3}$,
直线l的参数方程$\left\{\begin{array}{l}{x=-\sqrt{3}+tcos\frac{π}{6}}\\{y=-\frac{2\sqrt{3}}{3}+tsin\frac{π}{6}}\end{array}\right.$(t为参数);
(2)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,
圆化为直角坐标系的方程 x2+y2=4,
以直线l的参数方程代入圆的方程整理得到 t2+(-3-$\frac{2\sqrt{3}}{3}$)t+$\frac{13}{3}$=0 ①,
因为t1和t2是方程①的解,从而 t1t2=$\frac{13}{3}$.
所以,|PA|•|PB|=|t1t2|=$\frac{13}{3}$.
点评 本题考查直线的参数方程以及参数的几何意义,极坐标方程化为直角坐标方程,利用直线的参数方程中参数的几何意义是解题的关键.

练习册系列答案
相关题目
13.a,b,c是△ABC的三条边长,满足a4+b4=c4,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不确定 |
14.若函数f(x)=$\left\{\begin{array}{l}{{a}^{x},x<0}\\{(a-3)x+4a,x≥0}\end{array}\right.$(a>0,且a≠1)的值域为(-∞,+∞),则实数a的取值范围是( )
| A. | (3,+∞) | B. | (0,$\frac{1}{4}$] | C. | (1,3) | D. | [$\frac{1}{4}$,1) |
8.若a>b>0,c<d<0,则一定有( )
| A. | ac>bd | B. | ac<bd | C. | ad<bc | D. | ad>bc |
15.下列四个图形中,能表示函数y=f(x)的是( )
| A. | 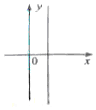 | B. | 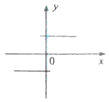 | C. | 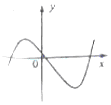 | D. | 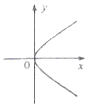 |
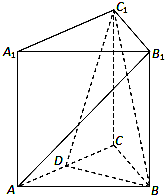 三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.
三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.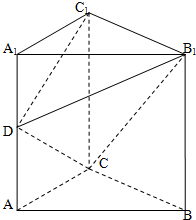 如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.
如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.