题目内容
3.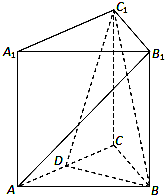 三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.
三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.(1)求证:平面BC1D⊥平面AA1CC1
(2)若AA1=AB=2,求点A到面BC1D的距离.
分析 (1)面面垂直转化为线面垂直,要证明平面BC1D⊥平面AA1CC1,只需证BD⊥平面AA1CC1即可.
(2)利用体积法求解.${V}_{A-B{C}_{1}D}={V}_{{C}_{1}-ABD}$,A1A⊥底面ABC,可得高为A1A.可得点A到面BC1D的距离
解答 解:(1)∵AA1⊥面ABC,AA1⊥BD,△ABC为正三角形,D为AC中点.易得BD⊥AC,
∴BD⊥面AA1CC1,又BD?面BC1D,
∴平面BC1D⊥平面AA1CC1
(2)由题意:AA1=AB=2,
∵${V}_{A-B{C}_{1}D}={V}_{{C}_{1}-ABD}$,A1A⊥⊥面ABC,
∴${V}_{{C}_{1}-ABD}$=△ABD×A1A=$\frac{1}{3}×\frac{1}{2}×2×2\sqrt{3}$=$\frac{2\sqrt{3}}{3}$
设点A到面BC1D的距离为h,
则:$\frac{1}{3}×\frac{1}{2}×\sqrt{3}×\sqrt{5}×h$=$\frac{2\sqrt{3}}{3}$
解得:h=$\frac{4\sqrt{5}}{5}$,
故得点A到面BC1D的距离为$\frac{4\sqrt{5}}{5}$.
点评 本题考查了面面垂直转化为线面垂直证明和利用体积法求解点到面的距离.属于中档题.

练习册系列答案
相关题目
2.若变量x,y满足约束条件$\left\{{\begin{array}{l}{x+y≥1}\\{y-x≤1}\\{x≤1}\end{array}}\right.$,则z=3x-2y的最小值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | -2 |
8.若方程sin2x+2sinx+a=0有解,则实数a的取值范围是( )
| A. | [-3,1] | B. | (-∞,1] | C. | [1,+∞) | D. | [-1,1] |
 已知直线l:4x+3y+15=0,半径为3的⊙C与l相切,圆心C在x轴上且在直线l的右上方.
已知直线l:4x+3y+15=0,半径为3的⊙C与l相切,圆心C在x轴上且在直线l的右上方.