题目内容
18.写出$\frac{{2}^{2}-1}{1}$,$\frac{{3}^{2}-2}{3}$,$\frac{{4}^{2}-3}{5}$,$\frac{{5}^{2}-4}{7}$,…的通项公式:$\frac{(n+1)^{2}-n}{2n-1}$..分析 分母是奇数可以表示为:2n-1;分子是项数加1的平方减1,即:(n+1)2-n.
解答 解:根据前四项的特点可以写出通项公式为:$\frac{(n+1)^{2}-n}{2n-1}$.
故答案为:$\frac{(n+1)^{2}-n}{2n-1}$.
点评 根据数列的前几项,写出数列的一个通项公式,考查的是学生对数据的观察归纳能力,需要注意其和常见数据的联系.

练习册系列答案
相关题目
10.把函数y=sinx的图象上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,再把图象向右平移$\frac{π}{6}$个单位,这是对应于这个图象的解析式为( )
| A. | $y=sin(2x-\frac{π}{3})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=sin(\frac{x}{2}-\frac{π}{3})$ | D. | $y=sin(\frac{x}{2}-\frac{π}{6})$ |
19.某校周四下午第五、六两节是选修课时间,现有甲、乙、丙三位教师可开课.已知甲、乙教师各自最多可以开设两节课,丙教师最多可以开设一节课.现要求第五、六两节课中每节课恰有两位教师开课(不必考虑教师所开课的班级和内容),则丙教师不开课的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
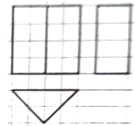 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积为32π.
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积为32π.