题目内容
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1的右焦点为F(c,0),一条渐近线为l,圆(x-c)2+y2=c2截直线l所得弦长为2$\sqrt{2}$,则该双曲线的实轴长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 由双曲线方程求出一条渐近线l的方程化为一般式,根据条件和弦长公式列出方程,化简后求出a的值,再求出该双曲线的实轴长.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线l的方程是y=$\frac{b}{a}x$,
即bx-ay=0,
因为圆(x-c)2+y2=c2截直线l所得弦长为2$\sqrt{2}$,
所以c2=${(\sqrt{2})}^{2}$+${(\frac{|bc-a×0|}{\sqrt{{b}^{2}+{a}^{2}}})}^{2}$,
化简得,c2=b2+2,则a=$\sqrt{2}$,
所以该双曲线的实轴长为2a=2$\sqrt{2}$,
故选:C.
点评 本题考查双曲线的简单几何性质,以及直线与圆相交时弦长问题,属于中档题.

练习册系列答案
相关题目
15.若θ∈(0,π),且sinθ+cosθ=$\frac{1}{5}$,则曲线$\frac{{x}^{2}}{sinθ}$+$\frac{{y}^{2}}{cosθ}$=1是( )
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
14.下列各组向量中不平行的是( )
| A. | $\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-2,-4,4) | B. | $\overrightarrow{c}$=(1,0,0),$\overrightarrow{d}$=(-3,0,0) | ||
| C. | $\overrightarrow{e}$=(2,3,0),$\overrightarrow{f}$=(0,0,0) | D. | $\overrightarrow{g}$=(-2,3,5)$\overrightarrow{h}$=(16,-24,40) |
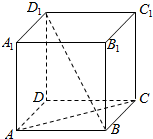 如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.