题目内容
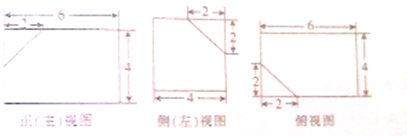
几何体的三视图如图，则该几何体的表面积为（ ）
A、122+
| ||
B、122+2
| ||
C、122+2
| ||
D、122+
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图，得出该几何体是长方体去掉一个三棱锥，画出图形，结合图形求出它的表面积即可．
解答：
解：根据几何体的三视图，得；
该几何体是长方体去掉一个三棱锥，如图所示，
长方体的长为6，宽为4，高为4，
∴该三棱锥的三条互相垂直的棱长为2，底面为边长2
的正三角形，
∴该几何体的表面积为
S表=2×6×4+2×4×4+2×6×4-3×
×2×2+
×2
×2
=122+2
．
故选：B．
该几何体是长方体去掉一个三棱锥，如图所示，
长方体的长为6，宽为4，高为4，
∴该三棱锥的三条互相垂直的棱长为2，底面为边长2
| 2 |
∴该几何体的表面积为
S表=2×6×4+2×4×4+2×6×4-3×
| 1 |
| 2 |
| ||
| 4 |
| 2 |
| 2 |
=122+2
| 3 |
故选：B．
点评：本题考查了空间几何体的三视图的应用问题，是基础题目．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
若椭圆
+
=1（a＞b＞0）的离心率为
，则双曲线
-
=1的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||
| B、y=±2x | ||
| C、y=±4x | ||
D、y=±
|
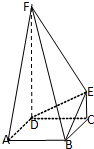如图，FD垂直于矩形ABCD所在平面，CE∥DF，∠DEF=90°．