题目内容
15.已知△ABC中,角A,B,C所对边分别为a,b,c,若$B=\frac{π}{6}$,$a=\sqrt{3}$,c=1,则b=1,△ABC的面积S=$\frac{{\sqrt{3}}}{4}$.分析 由已知利用余弦定理即可计算求得b的值,利用三角形面积公式即可计算得解△ABC的面积S.
解答 解:∵$B=\frac{π}{6}$,$a=\sqrt{3}$,c=1,
∴由余弦定理可得:b=$\sqrt{{a}^{2}+{c}^{2}-2accosB}$=$\sqrt{3+1-2×\sqrt{3}×1×cos\frac{π}{6}}$=1,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}×\sqrt{3}×1×sin\frac{π}{6}$=$\frac{\sqrt{3}}{4}$.
故答案为:1;$\frac{{\sqrt{3}}}{4}$.
点评 本题主要考查了余弦定理,三角形面积公式在解三角形中的应用,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.已知θ为第一象限的角,sinθ-2cosθ=-$\frac{2}{5}$,则sinθ+cosθ等于( )
| A. | $\frac{9}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{6}{5}$ |
4.复数z=3+$\frac{3+4i}{4-3i}$,则|z|等于( )
| A. | 3 | B. | $\sqrt{10}$ | C. | $\sqrt{13}$ | D. | 4 |
5.函数y=sinx•tanx的图象大致是( )
| A. |  | B. |  | C. |  | D. | 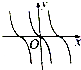 |
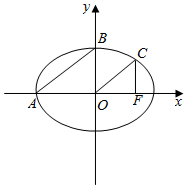 如图,A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,过椭圆的右焦点F作x轴的垂线,与其交于点C,若AB∥OC(O为坐标原点),则直线AB的斜率为$\frac{\sqrt{2}}{2}$.
如图,A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,过椭圆的右焦点F作x轴的垂线,与其交于点C,若AB∥OC(O为坐标原点),则直线AB的斜率为$\frac{\sqrt{2}}{2}$.