题目内容
求下列函数的定义域和值域
(1)y=2
;
(2)y=(
)-|x|;
(3)y=
;
(4)y=3
;
(5)=
;
(6)y=4x+2x+1.
(1)y=2
| 1 |
| 2x-4 |
(2)y=(
| 2 |
| 3 |
(3)y=
| 1-2x |
(4)y=3
| 2x-1 |
(5)=
(
|
(6)y=4x+2x+1.
考点:函数的值域,函数的定义域及其求法
专题:函数的性质及应用
分析:分别根据指数函数,二次函数以及二次根式的性质求出函数的定义域及值域.
解答:
解:(1)定义域为{x|x≠4}由y=2u的图象可知
令u=
≠0值域为{y|y>0,且y≠1}
(2)定义域为R,令u=-|x|≤0由y=(
)u的图象可知值域为{y|y≥1}
(3)由1-2x≥0,∴x≤0,∴定义域为{x|x≤0}
又∵2x>0,∴0≤1-2x<1,∴值域为[0,1)
(4)由2x-1≥0知定义域为{x|x≥
}
令u=
≥0,∴y=3u≥1,∴值域{y|y≥1}
(5)∵(
)x-1≥0,∴(
)x≥1,∴x≤0定义域为{x|x≤0}
又(
)x≥1故值域为{y|y≥0}
(6)定义域为R,y=(2x)2+2×2x+1令2x=u(u>0),
∴y=u2+2u+1=(u+1)2(u>0),∴y>1,
故值域为.{y|y>1}.
令u=
| 1 |
| x-4 |
(2)定义域为R,令u=-|x|≤0由y=(
| 2 |
| 3 |
(3)由1-2x≥0,∴x≤0,∴定义域为{x|x≤0}
又∵2x>0,∴0≤1-2x<1,∴值域为[0,1)
(4)由2x-1≥0知定义域为{x|x≥
| 1 |
| 2 |
令u=
| 2x-1 |
(5)∵(
| 1 |
| 3 |
| 1 |
| 3 |
又(
| 1 |
| 3 |
(6)定义域为R,y=(2x)2+2×2x+1令2x=u(u>0),
∴y=u2+2u+1=(u+1)2(u>0),∴y>1,
故值域为.{y|y>1}.
点评:本题考查了函数的定义域,值域问题,考查了指数函数,二次函数,二次根式的性质,是一道基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知点(1,-1)和(-2,1)在直线3x-2y-a=0的两侧,则a的取值范围是( )
| A、(-5,8) |
| B、(-8,5) |
| C、(-∞,-5)∪(8,+∞) |
| D、(-∞,-8)∪(5,+∞) |
已知集合A={x|x≥4},g(x)=
的定义域为B,若A∩B=∅,则实数a的取值范围是( )
| 1 | ||
|
| A、(-2,4) |
| B、(3,+∞) |
| C、(-∞,3) |
| D、(-∞,3] |
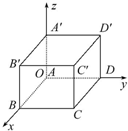 如图,已知长方体ABCD-A′B′C′D的边长为AB=12,AD=8,AA′=5.以这个长方体的顶点A为坐标原点,射线AB,AD,AA′分别为x轴、y轴、z轴的正半轴,建立空间直角坐标系,
如图,已知长方体ABCD-A′B′C′D的边长为AB=12,AD=8,AA′=5.以这个长方体的顶点A为坐标原点,射线AB,AD,AA′分别为x轴、y轴、z轴的正半轴,建立空间直角坐标系,