题目内容
已知-
<α<
,-
<β<
,且tanα,tanβ是方程x2+3
x+4=0的两实根,则α+β=( )
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:两角和与差的正切函数
专题:三角函数的求值
分析:由题意利用韦达定理可得 tanα+tanβ 和tanα•tanβ的值,可得 tan(α+β)=
的值.再根据α、β
的范围求得α+β的范围,从而求得α+β的值.
| tanα+tanβ |
| 1-tanα•tanβ |
的范围求得α+β的范围,从而求得α+β的值.
解答:
解:由题意可得 tanα+tanβ=-3
,tanα•tanβ=4,
∴tan(α+β)=
=
=
.
由已知-
<α<
,-
<β<
,可得-π<α+β<π,∴α+β=
,或α+β=-
,
故选:D.
| 3 |
∴tan(α+β)=
| tanα+tanβ |
| 1-tanα•tanβ |
-3
| ||
| 1-4 |
| 3 |
由已知-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
故选:D.
点评:本题主要考查两角和的正切公式的应用,根据三角函数的值求角,属于基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
常数列c,c,c,…,c,…( )
| A、一定是等差数列但不一定是等比数列 |
| B、一定是等比数列,但不一定是等差数列 |
| C、既一定是等差数列又一定是等比数列 |
| D、既不一定是等差数列,又不一定是等比数列 |
已知f(x)=
则f(2014)的值为( )
|
| A、-1 | B、0 | C、1 | D、2 |
设有穷数列{an}(n=1,2,…,n),Sn是其前n项和,定义
为{an}的“凯森和”.今有500项的数列a1,a2,…,a500的“凯森和”为2004,则有501项的数列2,a1,a2,…,a500的“凯森和”为( )
| S1+S2+…+Sn |
| n |
| A、2002 | B、2004 |
| C、2008 | D、2014 |
已知向量
=(n,1),
=(4,n),则n=2是
∥
的( )条件.
| a |
| b |
| a |
| b |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分又不要必 |
在直角坐标系中,已知点A(0,1)和点B(-3,4),若点P在∠AOB的平分线上且|
|=2,则点P的坐标为( )
| OP |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|
定义运算a*b=
,例如1*2=1,则2*a的取值范围是( )
|
| A、(0,2) |
| B、(-∞,2] |
| C、[0,2] |
| D、[2,+∞) |
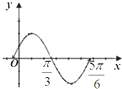
已知函数y=2sin(ωx+φ)(ω>0,|φ|<
)的图象的一部分如图所示,则( )
| π |
| 2 |

A、ω=2,φ=
| ||
B、ω=2,φ=-
| ||
C、ω=2,φ=
| ||
D、ω=2,φ=-
|