题目内容
设有穷数列{an}(n=1,2,…,n),Sn是其前n项和,定义
为{an}的“凯森和”.今有500项的数列a1,a2,…,a500的“凯森和”为2004,则有501项的数列2,a1,a2,…,a500的“凯森和”为( )
| S1+S2+…+Sn |
| n |
| A、2002 | B、2004 |
| C、2008 | D、2014 |
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件得
=2004,从而得到S1+S2+…+S500=2004×500,所以501项的数列2,a1,a2,…,a500的“凯森和”为
,由此能求出结果.
| S1+S2+…+S500 |
| 500 |
| 2×501+2004×500 |
| 501 |
解答:
解:∵500项的数列a1,a2,…,a500的“凯森和”为2004,
∴
=2004,
∴S1+S2+…+S500=2004×500,
∴501项的数列2,a1,a2,…,a500的“凯森和”为:
=
=
=2002.
故选:A.
∴
| S1+S2+…+S500 |
| 500 |
∴S1+S2+…+S500=2004×500,
∴501项的数列2,a1,a2,…,a500的“凯森和”为:
| 2+(2+S1)+(2+S2)+…+(2+S500) |
| 501 |
=
| 2×501+S1+S2+…+S500 |
| 501 |
=
| 2×501+2004×500 |
| 501 |
=2002.
故选:A.
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意新定义的正确理解.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
在△ABC中,角A,B,C的对边分别是a,b,c.已知a=5
,c=10,A=30°,则B等于( )
| 2 |
| A、105° |
| B、60° |
| C、15° |
| D、105° 或 15° |
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积为( )


| A、π+1 | ||
| B、4π+1 | ||
C、π+
| ||
D、4π+
|
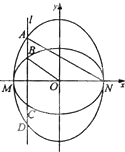 如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N在x轴上,椭圆C2的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点按纵坐标从大到小依次为A,B,C,D,且BO∥AN,则离心率e的范围是( )
如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N在x轴上,椭圆C2的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点按纵坐标从大到小依次为A,B,C,D,且BO∥AN,则离心率e的范围是( )A、
| ||||
B、0<e<
| ||||
C、0<e<
| ||||
D、
|
已知-
<α<
,-
<β<
,且tanα,tanβ是方程x2+3
x+4=0的两实根,则α+β=( )
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
等比数列{an}的公比为q,其前n项积为Tn,且满足a1>1,a99•a100-1>0,
<0.得出下列结论:(1)0<q<1;(2)a99•a100-1<0;(3)T100的值是Tn中最大的;(4)使Tn>1成立的最大自然数n等于198.其中正确的结论的个数为( )
| a99-1 |
| a100-1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
“α为锐角”是“sinα>0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |