题目内容
甲、乙两位同学参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取4次,绘制成茎叶图如图:
(Ⅰ)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由.
| 甲 | 乙 | |||||
| 9 | 7 | 7 | ||||
| 8 | 1 | 2 | 8 | 5 | 3 | 5 |
(Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由.
考点:茎叶图,众数、中位数、平均数,极差、方差与标准差
专题:概率与统计
分析:(I)由茎叶图知甲乙两同学的成绩分别为:甲:82 81 79 88 乙:85 77 83 85.利用“列举法”及其古典概型的概率计算公式即可得出.
(II)分别计算出甲乙的平均成绩及其方差即可得出.
(II)分别计算出甲乙的平均成绩及其方差即可得出.
解答:
解:(Ⅰ)由茎叶图知甲乙两同学的成绩分别为:
甲:82 81 79 88 乙:85 77 83 85
记从甲、乙两人的成绩中各随机抽取一个为(x,y),用列举法表示如下:(82,85),(82,77),(82,83),(82,85),(81,85),(81,77),(81,83),(81,85),(79,85),(79,77),(79,83),(79,85),(88,85),(88,77),(88,83),(88,85).
∴甲的成绩比乙高的概率为P=
.
(Ⅱ)派乙参赛比较合适,理由如下:甲的平均分
=82.5,乙的平均分
=82.5,甲乙平均分相同;
又甲的标准差的平方(即方差)
=15,乙的标准差的平方(即方差)
=14.33,
>
.
甲乙平均分相同,但乙的成绩比甲稳定,∴派乙去比较合适.
甲:82 81 79 88 乙:85 77 83 85
记从甲、乙两人的成绩中各随机抽取一个为(x,y),用列举法表示如下:(82,85),(82,77),(82,83),(82,85),(81,85),(81,77),(81,83),(81,85),(79,85),(79,77),(79,83),(79,85),(88,85),(88,77),(88,83),(88,85).
∴甲的成绩比乙高的概率为P=
| 7 |
| 16 |
(Ⅱ)派乙参赛比较合适,理由如下:甲的平均分
. |
| x甲 |
. |
| x乙 |
又甲的标准差的平方(即方差)
| S | 2 甲 |
| S | 2 乙 |
| S | 2 甲 |
| S | 2 乙 |
甲乙平均分相同,但乙的成绩比甲稳定,∴派乙去比较合适.
点评:本题考查了“列举法”及其古典概型的概率计算公式、平均数及其方差,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
已知数列{an}满足:a1=1,an+1=
(n∈N*).若bn+1=(n-2λ)•(
+1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围是( )
| an |
| an+2 |
| 1 |
| an |
A、λ>
| ||
B、λ>
| ||
C、λ<
| ||
D、λ<
|
已知x,y是正数,且满足2<x+2y<4.那么x2+y2的取值范围是( )
A、(
| ||||
B、(
| ||||
| C、(1,16) | ||||
D、(
|
设x=lnπ,y=log
,z=e-
,则( )
| 5 |
| 2 |
| 1 |
| 2 |
| A、y<z<x |
| B、z<x<y |
| C、z<y<x |
| D、x<y<z |
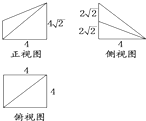 如图所示是一个几何体的三视图.正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).则该几何体的体积为
如图所示是一个几何体的三视图.正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).则该几何体的体积为