题目内容
NBA(美国职业篮球联赛)决赛实行7局制,比赛先胜4局者获得比赛的胜利(每局比赛都必须分出胜负,没有平局),比赛随即结束.除第七局甲队获胜的概率是
外,其余每局比赛甲队获胜的概率都是
,假设各局比赛结果相互独立.
(1)求甲队以4:0获得胜利的概率;
(2)若每局比赛胜利方得1分,对方得0分,求乙队最终比赛总得分X的分布列及数学期望.
| 1 |
| 2 |
| 2 |
| 3 |
(1)求甲队以4:0获得胜利的概率;
(2)若每局比赛胜利方得1分,对方得0分,求乙队最终比赛总得分X的分布列及数学期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)记“甲队以4:0胜利”为事件A,由题意,各局比赛结果相互独立,由此能求出甲队以4:0胜利的概率.
(2)由题意知,甲赢则乙输,由此知X的取值为0,1,2,3,4.分别求出相对应的概率,由此能求出X的分布列和E(X).
(2)由题意知,甲赢则乙输,由此知X的取值为0,1,2,3,4.分别求出相对应的概率,由此能求出X的分布列和E(X).
解答:
解:(1)记“甲队以4:0胜利”为事件A,由题意,各局比赛结果相互独立,
故P(A)=(
)4=
,
∴甲队以4:0胜利的概率是
.…2分
(2)由题意知,甲赢则乙输,可得X的取值可能为0,1,2,3,4.
P(X=0)=(
)4=
,
P(X=1)=
•
(
)3•
=
,…3分
P(X=2)=
(
)2(
)3•
=
,…4分
P(X=3)=
(
)3(
)3•
=
,…5分
P(X=4)=(
)4+
(
)(
)3(
)+
(
)2(
)3(
)+
(
)3(
)3(
)=
,…9分
故X的分布列为
∴E(X)=0×
+1×
+2×
+3×
+4×
=
=
.…10分.
故P(A)=(
| 2 |
| 3 |
| 16 |
| 81 |
∴甲队以4:0胜利的概率是
| 16 |
| 81 |
(2)由题意知,甲赢则乙输,可得X的取值可能为0,1,2,3,4.
P(X=0)=(
| 2 |
| 3 |
| 16 |
| 34 |
P(X=1)=
| C | 1 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 64 |
| 35 |
P(X=2)=
| C | 2 5 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 160 |
| 36 |
P(X=3)=
| C | 3 6 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 80 |
| 36 |
P(X=4)=(
| 1 |
| 3 |
| C | 1 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| C | 2 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| C | 3 6 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 153 |
| 36 |
故X的分布列为
| X | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 144 |
| 36 |
| 192 |
| 36 |
| 160 |
| 36 |
| 80 |
| 36 |
| 153 |
| 36 |
| 2604 |
| 37 |
| 1364 |
| 729 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
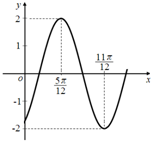 已知函数f(x)=Asin(ωx-
已知函数f(x)=Asin(ωx- 在平面直角坐标系xOy中,已知圆C经过A(2,-2),B(1,1)两点,且圆心在直线x-2y-2=0上.
在平面直角坐标系xOy中,已知圆C经过A(2,-2),B(1,1)两点,且圆心在直线x-2y-2=0上. 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,PA=3,AD=2,AB=4,∠ABC=60°.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,PA=3,AD=2,AB=4,∠ABC=60°.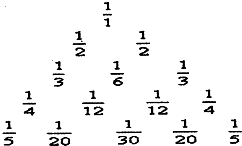 如图所示的三角形数阵叫”莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有死个数且两端的数均为告(砖≥2),每个数是它下一行左右相邻两数的和,如
如图所示的三角形数阵叫”莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有死个数且两端的数均为告(砖≥2),每个数是它下一行左右相邻两数的和,如