题目内容
20.已知抛物线y2=16x的准线过双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一个焦点,且双曲线的一条渐近线为$y=\sqrt{3}x$,则该双曲线的方程是$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$.分析 求出抛物线的准线方程,求出双曲线的焦点坐标,利用双曲线的渐近线方程,求出实半轴与虚半轴的长,得到双曲线方程即可.
解答 解:抛物线y2=16x的准线x=-4过双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一个焦点(-4,0),
双曲线的一条渐近线为$y=\sqrt{3}x$,可得b=$\sqrt{3}a$,c=$\sqrt{{a}^{2}+{b}^{2}}=4$,
解得a=2,b=2$\sqrt{3}$,
所求双曲线方程为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$.
故答案为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$.
点评 本题考查双曲线方程的求法,抛物线的简单性质以及双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
5.民大附中的甲、乙两人同时参加某大学的自主招生,在申请材料中提交了某学科10次的考试成绩(满分100分),按照时间顺序记录如下:

(1)根据两组数据画出两人成绩的茎叶图,并通过茎叶图比较两人成绩的平均值及分散程度(不要求计算具体值,直接写出结论即可);
(2)现将两人成绩分为三个等级:
注:A级高于B级,B级高于C级
假设两人的成绩相互独立,根据所给的数据,以事件发生的频率为相应事件发生的概率,求甲的等级高于乙的等级的概率;
(3)假如你是该大学的招生老师,结合上述数据,决定应录取哪位同学,说明理由.

(1)根据两组数据画出两人成绩的茎叶图,并通过茎叶图比较两人成绩的平均值及分散程度(不要求计算具体值,直接写出结论即可);
(2)现将两人成绩分为三个等级:
| 成绩分数 | [0,70] | [70,90] | [90,100] |
| 等级 | C级 | B级 | A级 |
假设两人的成绩相互独立,根据所给的数据,以事件发生的频率为相应事件发生的概率,求甲的等级高于乙的等级的概率;
(3)假如你是该大学的招生老师,结合上述数据,决定应录取哪位同学,说明理由.
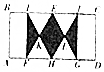 如图所示,已知长方形ABCD中,BC=2AB,△EFG与△HIJ均为等边三角形,F、H、G在AD上,I、E、J在BC上,连接FI,GJ,且AB∥FI∥GJ,若AF=GD,则向长方形ABCD内投掷一个点,该点落在阴影区域内的概率为$\frac{\sqrt{3}}{6}$.
如图所示,已知长方形ABCD中,BC=2AB,△EFG与△HIJ均为等边三角形,F、H、G在AD上,I、E、J在BC上,连接FI,GJ,且AB∥FI∥GJ,若AF=GD,则向长方形ABCD内投掷一个点,该点落在阴影区域内的概率为$\frac{\sqrt{3}}{6}$.