题目内容
9.已知函数f(x)=lnx+ax2-3x,且x=1在处函数取得极值.(1)求f(x)的单调区间;
(2)若g(x)=x2-2x-1(x>0)
①证明:g(x)的图象不能在y=f(x)图象的下方;
②证明不等式(2n+1)2>4ln(n!)恒成立.
分析 (1)先求函数的定义域,然后根据在x=1时函数f(x)取得极值求出a的值,最后根据f′(x)<0可求出函数的减区间,f′(x)>0可求出函数的增区间;
(2)①设F(x)=f(x)-g(x),利用导数研究函数F(x)的最大值,从而可判定F(x)的符号,即可证得g(x)的图象恒在f(x)图象的上方;
②由①可知,lnx-x+1≤0,可得lnx<x恒成立,从而有ln1<1,ln2<2,ln3<3,…,lnn<n,累加可得ln(1×2×3×…×n)=lnn!<$\frac{n(n+1)}{2}$,然后利用放缩法可证得结论.
解答 解:(1)由题可知,函数的定义域为{x|x>0},
f′(x)=$\frac{1}{x}$+2ax-3=$\frac{2{ax}^{2}-3x+1}{x}$,
∵x=1处函数f(x)取得极值.
∴f′(1)=0,即2a-3+1=0,解得a=1
即f′(x)=$\frac{(2x-1)(x-1)}{x}$,当x∈(0,$\frac{1}{2}$)时,f′(x)>0,
当x∈($\frac{1}{2}$,1)时,f′(x)<0,当x∈(1,+∞)时,f′(x)>0,
∴函数f(x)的单调增区间为(0,$\frac{1}{2}$),(1,+∞),函数f(x)的单调减区间为($\frac{1}{2}$,1);
(2)证明:①设F(x)=f(x)-g(x)=lnx-x+1,F′(x)=$\frac{1}{x}$-1=$\frac{1-x}{x}$,
∵当x∈(0,1)时,F′(x)>0,当x∈(1,+∞)时,F′(x)<0,
∴F(x)≤F(1)=0即f(x)<g(x)恒成立,
从而g(x)的图象不能在f(x)图象的上方;
②由①可知,lnx-x+1≤0,即lnx≤x-1∴lnx<x恒成立
从而有ln1<1,ln2<2,ln3<3,…,lnn<n,
累加得ln1+ln2+ln3+…+lnn<1+2+3+…+n
即ln(1×2×3×…×n)=lnn!<$\frac{n(n+1)}{2}$,
∵$\frac{n(n+1)}{2}$<( $\frac{n+n+1}{2}$)2,
∴$\frac{{(2n+1)}^{2}}{4}$>ln(n!)即(2n+1)2>4ln(n!).
点评 本题主要考查了函数的单调性和恒成立问题以及不等式的证明,同时考查了计算能力,属于中档题.


(1)根据两组数据画出两人成绩的茎叶图,并通过茎叶图比较两人成绩的平均值及分散程度(不要求计算具体值,直接写出结论即可);
(2)现将两人成绩分为三个等级:
| 成绩分数 | [0,70] | [70,90] | [90,100] |
| 等级 | C级 | B级 | A级 |
假设两人的成绩相互独立,根据所给的数据,以事件发生的频率为相应事件发生的概率,求甲的等级高于乙的等级的概率;
(3)假如你是该大学的招生老师,结合上述数据,决定应录取哪位同学,说明理由.
| A. | (¬p)∧(¬q) | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | b<c<a |
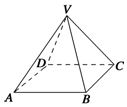 如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.