题目内容
已知A={2,a},B={1,2,3},则“a=3”是“A⊆B”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分亦非必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充要条件的定义,分析“a=3”⇒“A⊆B”,与“a=3”?“A⊆B”的真假,进而得到答案.
解答:
解:当“a=3”时,A={2,3},B={1,2,3},
此时“A⊆B”,故“a=3”是“A⊆B”的充分条件;
若“A⊆B”时,a=1,或a=3,
故“a=3”是“A⊆B”的不必要条件;
综上“a=3”是“A⊆B”的充分不必要条件;
故选:A
此时“A⊆B”,故“a=3”是“A⊆B”的充分条件;
若“A⊆B”时,a=1,或a=3,
故“a=3”是“A⊆B”的不必要条件;
综上“a=3”是“A⊆B”的充分不必要条件;
故选:A
点评:本题考查的知识点是充要条件,熟练掌握充要条件的定义是解答的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
有50件产品,编号为00,01,02,03,…,49.现从中抽取5件进行检验,用系统抽样方法所抽取样本的编号可以是( )
| A、05,10,15,20,25 |
| B、05,14,22,30,38 |
| C、08,22,23,31,40 |
| D、00,10,20,30,40 |
已知三角形ABC的三个内角A﹑B﹑C对边分别为a﹑b﹑c,则下列数值中,一定能构成三角形的三边的是( )
| A、a2﹑b2﹑c2 | ||||||||
B、
| ||||||||
C、1+
| ||||||||
| D、sinA﹑sinB﹑sinC |
若集合A={0,2,3,5},则集合A的真子集共有( )
| A、7个 | B、8个 |
| C、15个 | D、16个 |
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为( )
| α |
A、
| ||
B、
| ||
C、
| ||
D、
|
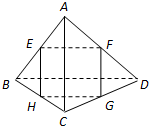 如图,空间四边形ABCD中,E,F,G,H分别为BA,AD,DC,CB边上的中点.则下列说法中不正确的是( )
如图,空间四边形ABCD中,E,F,G,H分别为BA,AD,DC,CB边上的中点.则下列说法中不正确的是( )| A、四边形EFGH为平行四边形 |
| B、直线AC∥平面EFGH |
| C、若棱AC=BD,则四边形EFGH为矩形 |
| D、若棱AC=BD,则四边形EFGH为菱形 |
已知L1:x-3y+7=0,L2:x+2y+4=0,下列说法正确的是( )
A、L1到L2的角为
| ||
B、L1到L2的角为
| ||
C、L2到L1的角为
| ||
D、L1到L2的夹角为
|