题目内容
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为( )
| α |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:本题是一个古典概型,a的取法有2种,b的取法有2种,得到可以组成向量的个数,从中任取两个向量共C42种取法,再由列举法求出面积等于1的三角形的个数,根据概率公式得到结果.
解答:
解:由题意知本题是一个古典概型,
试验发生包含的事件是取出数字,构成向量,
a的取法有2种,b的取法有2种,故向量
=(a,b)有4个,
从中任取两个向量共C42=6种取法,
由满足条件的事件列举法求出面积等于1的三角形的个数有2个,
∴根据古典概型概率公式得到P=
=
,
故选:B.
试验发生包含的事件是取出数字,构成向量,
a的取法有2种,b的取法有2种,故向量
| α |
从中任取两个向量共C42=6种取法,
由满足条件的事件列举法求出面积等于1的三角形的个数有2个,
∴根据古典概型概率公式得到P=
| 2 |
| 6 |
| 1 |
| 3 |
故选:B.
点评:本题考查古典概型及其概率计算公式,考查组合数问题、考查三角形面积问题,注意列举法在解题中的作用.

练习册系列答案
相关题目
若x,y均为区间(0,1)的随机数,则2x-y>0的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在下列命题中,正确命题的个数是( )
①两个复数不能比较大小;
②复数z=i-1对应的点在第四象限;
③若(x2-1)+(x2+3x+2)i是纯虚数,则实数x=±1;
④若(z1-z2)2+(z2-z3)2=0,则z1=z2=z3.
①两个复数不能比较大小;
②复数z=i-1对应的点在第四象限;
③若(x2-1)+(x2+3x+2)i是纯虚数,则实数x=±1;
④若(z1-z2)2+(z2-z3)2=0,则z1=z2=z3.
| A、0 | B、1 | C、2 | D、3 |
已知A={2,a},B={1,2,3},则“a=3”是“A⊆B”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分亦非必要条件 |
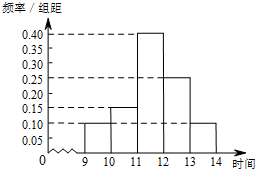 某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )
某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )| A、8万元 | B、10万元 |
| C、12万元 | D、15万 |
一个几何体的三视图如图所示,则这个几何体的表面积为( )


A、7+
| ||
B、9+
| ||
C、7+
| ||
D、9+
|