题目内容
已知两条直线l1:x+(1+m)y=2-m,l2:2mx+4y=-16,m为何值时,l1与l2:(1)平行 (2)垂直.
考点:直线的一般式方程与直线的平行关系,直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:(1)解1×4-(1+m)(2m)=0,排除两直线重合即可;(2)由垂直关系可得1×2m+4(1+m)=0,解方程可得.
解答:
解:(1)∵l1:x+(1+m)y=2-m,l2:2mx+4y=-16,
∴1×4-(1+m)(2m)=0,解得m=1或m=-2,
当m=-2时,两直线重合,当m=1时两直线平行;
(2)由垂直关系可得1×2m+4(1+m)=0,
解得m=-
,
∴当m=-
时,两直线垂直.
∴1×4-(1+m)(2m)=0,解得m=1或m=-2,
当m=-2时,两直线重合,当m=1时两直线平行;
(2)由垂直关系可得1×2m+4(1+m)=0,
解得m=-
| 2 |
| 3 |
∴当m=-
| 2 |
| 3 |
点评:本题考查直线的一般式方程和平行垂直关系,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=3x-x3的单调递增区间是( )
| A、[-1,1] | ||||
| B、[1,+∞)∪(-∞,-1] | ||||
| C、[1,+∞)及(-∞,-1] | ||||
D、[-
|
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为x-2y=0,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 三棱柱ABC-A1B1C1体积为V,M是AA1中点,求四棱锥M-BCC1B1的体积.
三棱柱ABC-A1B1C1体积为V,M是AA1中点,求四棱锥M-BCC1B1的体积.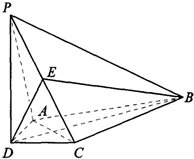 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E是PC的中点,AD=CD=1,
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E是PC的中点,AD=CD=1,