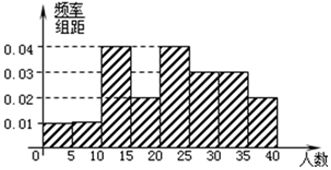
题目内容
2.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两焦点为F1,F2,A,B分别是椭圆的左顶点和上顶点,若线段AB上存在点P,使PF1⊥PF2,则椭圆的离心率的取值范围为$[\frac{\sqrt{5}-1}{2},\frac{\sqrt{2}}{2}]$.分析 依题意,作图如下:A(-a,0),B(0,b),F1(-c,0),F2(c,0),直线AB的方程为:bx-ay+ab=0,设直线AB上的点P(x,y),则bx=ay-ab,由PF1⊥PF2,$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=x2+y2-c2=$(\frac{a}{b}y-a)^{2}$+y2-c2=f(y),令f′(y)=2$\frac{a}{b}$$(\frac{a}{b}y-a)$+2y=0,解得:y=$\frac{{a}^{2}b}{{a}^{2}+{b}^{2}}$,x=-$\frac{a{b}^{2}}{{a}^{2}+{b}^{2}}$,满足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,解得e=$\frac{\sqrt{5}-1}{2}$,为最小值.当点P取B时,b=c,e=$\frac{\sqrt{2}}{2}$取得最大值.即可得出.
解答 解:依题意,作图如下: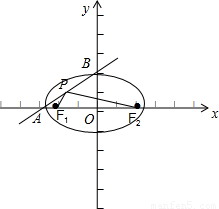
∵A(-a,0),B(0,b),F1(-c,0),F2(c,0),
∴直线AB的方程为:$\frac{x}{-a}$+$\frac{y}{b}$=1.整理得:bx-ay+ab=0,
设直线AB上的点P(x,y)
则bx=ay-ab,
∴x=$\frac{a}{b}$y-a,
∵PF1⊥PF2,
∴$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=(-c-x,-y)•(c-x,-y)=x2+y2-c2
=$(\frac{a}{b}y-a)^{2}$+y2-c2=f(y),
令f′(y)=2$\frac{a}{b}$$(\frac{a}{b}y-a)$+2y=0,
∴由f′(y)=0得:y=$\frac{{a}^{2}b}{{a}^{2}+{b}^{2}}$,于是x=-$\frac{a{b}^{2}}{{a}^{2}+{b}^{2}}$,
∴$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=$(-\frac{a{b}^{2}}{{a}^{2}+{b}^{2}})^{2}+(\frac{{a}^{2}b}{{a}^{2}+{b}^{2}})^{2}$-c2=0,
整理可得:$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$=c2,又b2=a2-c2,e2=$\frac{{c}^{2}}{{a}^{2}}$,
∴e4-3e2+1=0,
∴e2=$\frac{3-\sqrt{5}}{2}$,又椭圆的离心率e∈(0,1),
∴e=$\frac{\sqrt{5}-1}{2}$,为最小值.
当点P取B时,b=c,e=$\frac{\sqrt{2}}{2}$.
∴椭圆的离心率的取值范围为$[\frac{\sqrt{5}-1}{2},\frac{\sqrt{2}}{2}]$.
故答案为:$[\frac{\sqrt{5}-1}{2},\frac{\sqrt{2}}{2}]$.
点评 本题考查了椭圆的标准方程及其性质、利用导数研究函数的单调性、数量积运算性质,考查了推理能力与计算能力,属于难题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |