题目内容
11.已知数列${a_1}=1,{a_2}=5,{a_{n+2}}={a_{n+1}}-{a_n}({n∈{N^*}})$,则a2016=( )| A. | 1 | B. | 4 | C. | -4 | D. | 5 |
分析 数列${a_1}=1,{a_2}=5,{a_{n+2}}={a_{n+1}}-{a_n}({n∈{N^*}})$,可得:an+6=an.即可得出.
解答 解:数列${a_1}=1,{a_2}=5,{a_{n+2}}={a_{n+1}}-{a_n}({n∈{N^*}})$,∴a3=a2-a1=4,同理可得:a4=-1,a5=-5,a6=-4,a7=1,a8=5,…,
可得an+6=an.
则a2016=a335×6+6=a6=-4.
故选:C.
点评 本题考查了数列递推关系、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.若点P(3,1)为圆(x-2)2+y2=16的弦AB的中点,则直线AB的方程为( )
| A. | x-3y=0 | B. | 2x-y-5=0 | C. | x+y-4=0 | D. | x-2y-1=0 |
3.已知某品种的幼苗每株成活率为p,则栽种3株这种幼苗恰好成活2株的概率为( )
| A. | p2 | B. | p2(1-p) | C. | ${C}_{3}^{2}$p2 | D. | ${C}_{3}^{2}$p2(1-p) |
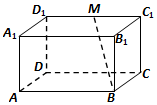 如图,在长方体ABCD-A1B1C1D1中,AB=2AD=4,A A1=2$\sqrt{2}$,M是C1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=2AD=4,A A1=2$\sqrt{2}$,M是C1D1的中点. 2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下:
2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下: