题目内容
已知函数f（x）=（x-1）（x-2）（x-3）…（x-98）（x-99）（x-100），则f′（99）= ．
考点：导数的运算
专题：导数的概念及应用
分析：将函数f（x）分成两组，利用导数的运算法则进行求解即可．
解答：
解：f′（x）=（x-99）′[（x-1）（x-2）（x-3）…（x-98）（x-100）]+（x-99）[（x-1）（x-2）（x-3）…（x-98）（x-99）（x-100）]′
=[（x-1）（x-2）（x-3）…（x-98）（x-100）]+（x-99）[（x-1）（x-2）（x-3）…（x-98）（x-99）（x-100）]′
则f′（99）=[（99-1）（99-2）（99-3）…（99-98）（99-100）]=-1×1×2×…×98=-98!，
故答案为：-98!
=[（x-1）（x-2）（x-3）…（x-98）（x-100）]+（x-99）[（x-1）（x-2）（x-3）…（x-98）（x-99）（x-100）]′
则f′（99）=[（99-1）（99-2）（99-3）…（99-98）（99-100）]=-1×1×2×…×98=-98!，
故答案为：-98!
点评：本题主要考查导数的计算，根据函数积的导数公式将函数分成两组是解决本题的关键．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
对任意非零实数a，b，若a?b的运算法则如图的框图所示，则4?（lg100）的值等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
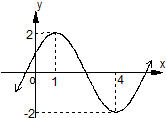已知简谐运动f（x）=Asin（ωx+φ），（|φ|＜| π |
| 2 |
则该简谐运动的最小正周期和初相φ分别为（ ）
A、T=6，φ=
| ||
B、T=6，φ=
| ||
C、T=6，φ=
| ||
D、T=6，φ=
|
在△ABC中，角A，B，C的对边分别为a，b，c，且b2+a2=c2+
ab，则内角C=（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|