题目内容
若函数f(x)的图象在(0,+∞)上是连续不断的,且在区间(2,3)内有惟一的无理数零点x0,那么用“二分法”求精确度为0.001的x0的近似值时,需要计算 次区间中点的函数值.
考点:二分法求方程的近似解
专题:计算题
分析:每一次二等分都使区间的长度变为原来的一半,区间 (1,2)的长度等于1,二分9次后,区间(1,2)长度变为
,满足精度要求,从而得到结论.
| 1 |
| 1024 |
解答:
解:每一次二等分都使区间的长度变为原来的一半,区间 (1,2)的长度等于1,
二分3次后,区间(1,2)长度变为
=
>
,不满足精度要求.
二分4次后,区间(1,2)长度变为
=
>
,不满足精度要求.
…
二分9次后,区间(1,2)长度变为
=
<
,满足精度要求.
故二分的次数至多有9次,
故答案为:9.
二分3次后,区间(1,2)长度变为
| 1 |
| 23 |
| 1 |
| 8 |
| 1 |
| 1000 |
二分4次后,区间(1,2)长度变为
| 1 |
| 24 |
| 1 |
| 16 |
| 1 |
| 1000 |
…
二分9次后,区间(1,2)长度变为
| 1 |
| 29 |
| 1 |
| 1024 |
| 1 |
| 1000 |
故二分的次数至多有9次,
故答案为:9.
点评:本题主要考查用二分法求方程的近似解,注意利用每一次二等分都使区间的长度变为原来的一半,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
袋子中放有大小和形状相同的4个小球,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球2个,从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b,记事件A表示“a+b=2”,则事件A的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数y=x2-3x-4的定义域为[0,m],值域为[-
,-4],则m的取值范围是( )
| 25 |
| 4 |
| A、(0,4] | ||
B、[
| ||
C、[
| ||
D、[
|
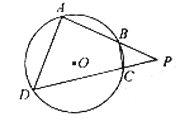 如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若PB=1,PD=3,则
如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若PB=1,PD=3,则