题目内容
已知函数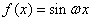
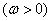 在区间
在区间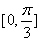 上单调递增,在区间
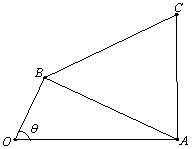
上单调递增,在区间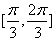 上单调递减;如图,四边形
上单调递减;如图,四边形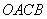 中,
中,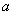 ,
,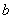 ,
,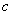 为
为 的内角
的内角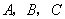 的对边,且满足
的对边,且满足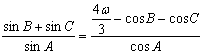 .
.
(Ⅰ)证明: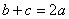 ;
;
(Ⅱ)若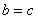 ,设
,设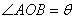 ,
,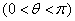 ,
,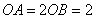 ,
,
求四边形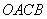 面积的最大值.
面积的最大值.
 |
解析:(Ⅰ)由题意知: ,解得:
,解得: ,
,





(Ⅱ)因为 ,所以
,所以 ,所以
,所以 为等边三角形
为等边三角形



 ,
,
 ,
, ,
,
当且仅当 即
即 时取最大值,
时取最大值, 的最大值为
的最大值为 .
.

练习册系列答案
相关题目
题目内容
已知函数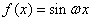
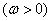 在区间
在区间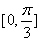 上单调递增,在区间
上单调递增,在区间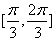 上单调递减;如图,四边形
上单调递减;如图,四边形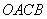 中,
中,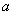 ,
,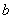 ,
,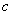 为
为 的内角
的内角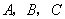 的对边,且满足
的对边,且满足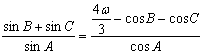 .
.
(Ⅰ)证明: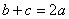 ;
;
(Ⅱ)若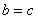 ,设
,设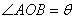 ,
,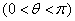 ,
,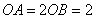 ,
,
求四边形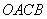 面积的最大值.
面积的最大值.
 |
解析:(Ⅰ)由题意知: ,解得:
,解得: ,
,





(Ⅱ)因为 ,所以
,所以 ,所以
,所以 为等边三角形
为等边三角形



 ,
,
 ,
, ,
,
当且仅当 即
即 时取最大值,
时取最大值, 的最大值为
的最大值为 .
.
