题目内容
已知函数f(x)=sin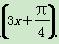
(1)求f(x)的单调递增区间;
(2)若α是第二象限角,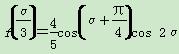 ,求cos α-sin α的值.
,求cos α-sin α的值.
解:(1)因为函数y=sin x的单调递增区间为 ,k∈Z,
,k∈Z,
 (cos2 α-sin2 α),
(cos2 α-sin2 α),
即sin α+cos α=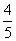 (cos α-sin α)2(sin α+cos α).
(cos α-sin α)2(sin α+cos α).
当sin α+cos α=0时,由α是第二象限角,
得α= +2kπ,k∈Z,
+2kπ,k∈Z,
此时,cos α-sin α=-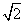 .
.
当sin α+cos α≠0时,(cos α-sin α)2= .
.
由α是第二象限角,得cos α-sin α<0,此时cos α-sin α=- .
.
综上所述,cos α-sin α=-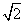 或-
或- .
.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
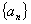 的各项都是正数,且对任意
的各项都是正数,且对任意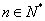 ,都有
,都有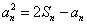 ,,其中
,,其中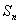 为数列
为数列 (
(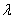 为非零整数,
为非零整数,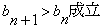 .
. ,
, .
. 时,求
时,求 的单调区间;
的单调区间;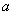 ,证明:
,证明: .
.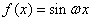
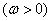 在区间
在区间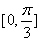 上单调递增,在区间
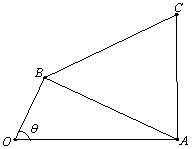
上单调递增,在区间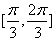 上单调递减;如图,四边形
上单调递减;如图,四边形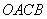 中,
中,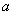 ,
,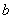 ,
,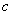 为
为 的内角
的内角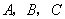 的对边,且满足
的对边,且满足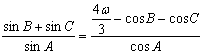 .
.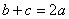 ;
;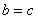 ,设
,设 ,
, ,
, ,
,
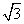 cos
cos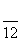 t-sin
t-sin 的值.
的值.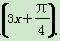
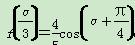 cos 2α,求cos α-sin α的值.
cos 2α,求cos α-sin α的值.