��Ŀ����
��֪����f��x��=
g��x��=asin��
x+
��-2a+2��a��0�����������н��ۣ�
���ۣ�
�ٺ���f��x����ֵ��Ϊ[0��
]��
�ں���g��x����[0��1]������������
�۶�����a��0������f��x��=g��x����[0��1]�ں��н⣻
��������x1��x2��[0��1]��ʹ��f��x1��=g��x2����������ʵ��a��ȡֵ��Χ��[
��
]��
����������ȷ���۵������ ��
|
| �� |
| 3 |
| 3�� |
| 2 |
���ۣ�
�ٺ���f��x����ֵ��Ϊ[0��
| 2 |
| 3 |
�ں���g��x����[0��1]������������
�۶�����a��0������f��x��=g��x����[0��1]�ں��н⣻
��������x1��x2��[0��1]��ʹ��f��x1��=g��x2����������ʵ��a��ȡֵ��Χ��[
| 4 |
| 9 |
| 4 |
| 5 |
����������ȷ���۵������
���㣺�ֶκ�����Ӧ��
ר�⣺�Ķ���,���������ʼ�Ӧ��
���������f��x���ĸ��ε�ֵ�������������жϢ٣�����g��x�����ж�g��x���ĵ����Լ����жϢڣ�
���g��x����[0��1]��ֵ���������f��x��=g��x����[0��1]�����a�ķ�Χ�������жϢۣ�
�ɢ۵ã��н������Ϊ��g��x������Сֵ������f��x�������ֵ��g��x�������ֵ��С��f��x������Сֵ�����a�ķ�Χ�������жϢܣ�
���g��x����[0��1]��ֵ���������f��x��=g��x����[0��1]�����a�ķ�Χ�������жϢۣ�
�ɢ۵ã��н������Ϊ��g��x������Сֵ������f��x�������ֵ��g��x�������ֵ��С��f��x������Сֵ�����a�ķ�Χ�������жϢܣ�
���
�⣺��x��[0��
]ʱ��f��x��=
-
x�ǵݼ���������f��x����[0��
]��
��x�ʣ�
��1]ʱ��f��x��=
=2��x+2��+
-8��f�䣨x��=2-
��0����f��x���ڣ�
��1]�ϵ�����
��f��x���ʣ�
��
]��
��x��[0��1]ʱ��f��x����[0��
]���ʢ���ȷ��
��x��[0��1]ʱ��g��x��=asin��
x+
��-2a+2��a��0��=-acos
x-2a+2��
��a��0��0��
x��
����g��x����[0��1]���ǵ����������ʢ���ȷ��
�ɢ�֪��a��0��x��[0��1]ʱg��x����[2-3a��2-
]��
��2-3a��
��2-
��0����0��a��
��a��
������f��x��=g��x����[0��1]���⣬�ʢ۴���
�ʴ���x1��x2��[0��1]��ʹ��f��x1��=g��x2����������
���
��a��
��
�ʢ���ȷ��
�ʴ�Ϊ���٢ڢܣ�
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
��x�ʣ�
| 1 |
| 2 |
| 2x2 |
| x+2 |
| 8 |
| x+2 |
| 8 |
| (x+2)2 |
| 1 |
| 2 |
��f��x���ʣ�
| 1 |
| 5 |
| 2 |
| 3 |
��x��[0��1]ʱ��f��x����[0��
| 2 |
| 3 |
��x��[0��1]ʱ��g��x��=asin��
| �� |
| 3 |
| 3�� |
| 2 |
| �� |
| 3 |
��a��0��0��
| �� |
| 3 |
| �� |
| 3 |
�ɢ�֪��a��0��x��[0��1]ʱg��x����[2-3a��2-
| 5a |
| 2 |
��2-3a��
| 2 |
| 3 |
| 5a |
| 2 |
| 4 |
| 9 |
| 4 |
| 5 |
�ʴ���x1��x2��[0��1]��ʹ��f��x1��=g��x2����������
|
| 4 |
| 9 |
| 4 |
| 5 |
�ʢ���ȷ��
�ʴ�Ϊ���٢ڢܣ�
���������⿼��ֶκ��������ã����麯����ֵ��͵����Լ����ã�������������������������ת��Ϊ��ֵ֮��Ĺ�ϵ�������״�����е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
�ڡ�ABC�У�A=60�㣬b=1��S��ABC=
����
=��������
| 3 |
| a+b+c |
| sinA+sinB+sinC |
A��
| ||||
B��
| ||||
C��
| ||||
D��2
|
����f��x��=2x+sinx�IJ���ͼ������ǣ�������
A�� |
B�� |
C�� |
D�� |
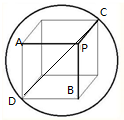 ��ͼ����֪��O�����������ĵ�P��A��B��C����PC��PA��PB������ֱ��PC=5��PA=3��PB=4������C���ֱ��ΪCD��������P-CD-A�Ĵ�С��
��ͼ����֪��O�����������ĵ�P��A��B��C����PC��PA��PB������ֱ��PC=5��PA=3��PB=4������C���ֱ��ΪCD��������P-CD-A�Ĵ�С��