题目内容
AB为单位圆上的弦,P为单位圆上的动点,设f(λ)=|
-λ
|的最小值为M,若M的最大值Mmax=
,则|
|的值等于 .
| BP |
| BA |
| 3 |
| 2 |
| AB |
考点:平面向量的综合题
专题:计算题,平面向量及应用
分析:设λ
=
,则f(λ)=|
-λ
|=|
|,点C在直线AB上,故f(λ)的最小值M为点P到AB的距离,由此可得结论.
| BA |
| BC |
| BP |
| BA |
| CP |
解答:
解:设λ
=
,则f(λ)=|
-λ
|=|
|,
∵λ
=
,∴点C在直线AB上,
∴f(λ)的最小值M为点P到AB的距离,
∵Mmax=
,
∴|
|=2
=
故答案为:
.
| BA |
| BC |
| BP |
| BA |
| CP |
∵λ
| BA |
| BC |
∴f(λ)的最小值M为点P到AB的距离,
∵Mmax=
| 3 |
| 2 |
∴|
| AB |
1-(
|
| 3 |
故答案为:
| 3 |
点评:本题考查向量知识的运用,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
设F是双曲线
-
=1(a>0,b>0)的左焦点,A(a,b),P是双曲线右支上的动点.若|PF|+|PA|的最小值为3a,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、1+
| ||||
C、
| ||||
D、
|
把函数y=f(x)的图象向右平移
个单位,然后将图象上的所有点的横坐标缩短到原来的一半(纵坐标不变)得到函数y=cosx的图象,则函数y=f(x)的解析式为( )
| π |
| 4 |
A、y=cos(
| ||||
B、y=cos(2x+
| ||||
C、y=cos(
| ||||
D、y=cos(2x+
|
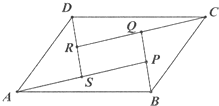 如图,在平行四边形ABCD中,设
如图,在平行四边形ABCD中,设