题目内容
求下列函数的值域:
(1)y=x3;
(2)y=x
.
(1)y=x3;
(2)y=x
| 1 |
| 2 |
考点:函数的值域
专题:函数的性质及应用
分析:(1)分别让x趋向正无穷和负无穷,看函数值y的取值情况,即可求出该函数的值域;
(2)首先x
≥0,然后说明x趋向正无穷时y的取值情况即可求出该函数的值域.
(2)首先x
| 1 |
| 2 |
解答:
解:(1)当x向右趋向正无穷时,x3趋向正无穷;
当x向左趋向负无穷时,x3趋向负无穷,所以:
该函数y=x3的值域为(-∞,+∞);
(2)∵x
≥0,即y≥0,当x趋向正无穷时,y也趋向正无穷;
∴函数y=x
的值域为[0,+∞).
当x向左趋向负无穷时,x3趋向负无穷,所以:
该函数y=x3的值域为(-∞,+∞);
(2)∵x
| 1 |
| 2 |
∴函数y=x
| 1 |
| 2 |
点评:考查函数值域的概念,通过观察函数解析式形式,让x取遍定义域时,判断函数y的取值情况的求值域方法,这两个函数的值域也可通过函数的图象来说明.

练习册系列答案
相关题目
直线3x-4y+6=0与圆(x-2)2+(y-3)2=4的位置关系是( )
| A、直线与圆相交且过圆心 |
| B、直线与圆相交但不过圆心 |
| C、相切 |
| D、相离 |
把函数y=f(x)的图象向右平移
个单位,然后将图象上的所有点的横坐标缩短到原来的一半(纵坐标不变)得到函数y=cosx的图象,则函数y=f(x)的解析式为( )
| π |
| 4 |
A、y=cos(
| ||||
B、y=cos(2x+
| ||||
C、y=cos(
| ||||
D、y=cos(2x+
|
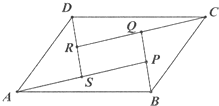 如图,在平行四边形ABCD中,设
如图,在平行四边形ABCD中,设