题目内容
若函数f(x)是偶函数,对任意x∈R都有f(x+2)=f(x),且x∈[-1,0]时,f(x)=-x,则方程f(x)=lgx的实根个数为 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:先证明函数f(x)的周期性,再利用函数周期性画出函数f(x)的图象,在同一直角坐标系下再画出函数y=lgx的图象,数形结合即可求得交点个数
解答:
解:∵f(x+1)=-x,
∴f(x+2)=f(x),∴函数f(x)为周期为2的周期函数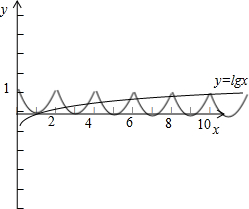 ,
,
∵x∈[-1,0]时,f(x)=-x,
∴函数f(x)的图象和y=lgx的图象如图:
由图数形结合可得函数y=f(x)与函数y=lgx的图象的交点个数为9个,
故答案为:9.
∴f(x+2)=f(x),∴函数f(x)为周期为2的周期函数
 ,
,∵x∈[-1,0]时,f(x)=-x,
∴函数f(x)的图象和y=lgx的图象如图:
由图数形结合可得函数y=f(x)与函数y=lgx的图象的交点个数为9个,
故答案为:9.
点评:本题主要考查了利用函数图象数形结合解决图象交点问题的方法,利用函数的周期性画周期函数的图象,对数函数的图象和性质.

练习册系列答案
相关题目
近期由于某些原因,国内进口豪华轿车纷纷降价,某豪车原价为200万元,连续两次降价a%后,售价为148万元,则下面所列方程正确的是( )
| A、200(1+a%)2=148 |
| B、200(1-a%)2=148 |
| C、200(1-2a%)=148 |
| D、200(1-a%)=148 |
设函数f(x)是偶函数,且当x>0时,f(x)=
,则在区间[-4,-2]内,函数f(x)( )
| 2 |
| x+1 |
A、单调递增,最大值
| ||
B、单调递减,最大值
| ||
C、单调递增,最小值
| ||
D、单调递增,最大值
|
若a<0,点p(-a2-1,-a+3)关于原点的对称点为p1,则p1在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在等差数列{an}中,若
=13,则
=( )
| a4 |
| a7 |
| S7 |
| S13 |
| A、7 | ||
| B、13 | ||
C、
| ||
D、
|
已知sinα•cosα=
,且
<α<
,则cosα-sinα=( )
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 在三棱锥A-BCD中,底面BCD是正三角形,AC=BD=2,AB=AD=
在三棱锥A-BCD中,底面BCD是正三角形,AC=BD=2,AB=AD=