题目内容
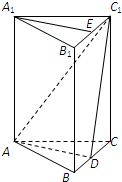如图，在直三棱柱ABC-A1B1C1中，AB=AC，点D为BC中点，点E在线段B1C1上．（1）求证：平面ADC1⊥平面BCC1B1；
（2）若A1E∥平面ADC1，求证：E为线段B1C1的中点．
考点：平面与平面垂直的判定,直线与平面平行的性质
专题：证明题,空间位置关系与距离
分析：（1）要证平面ADC1⊥平面BCC1B1，只需证平面ADC1内的直线AD⊥平面BCC1B1，即证AD垂直平面BCC1B1内的两条相交直线CC1、BC即可；
（2）设点E′是B1C1的中点．通过（1）AD⊥BC，D为BC边上的中点，连接DE′，则四边形B1BDE′为平行四边形，可证四边形A1ADE为平行四边形，从而A1E′∥AD，又A1E′?平面ADC1，AD?平面ADC1，根据线面平行的判定定理可知A1E′∥平面ADC1，E与E′重合，即可得出结论．
（2）设点E′是B1C1的中点．通过（1）AD⊥BC，D为BC边上的中点，连接DE′，则四边形B1BDE′为平行四边形，可证四边形A1ADE为平行四边形，从而A1E′∥AD，又A1E′?平面ADC1，AD?平面ADC1，根据线面平行的判定定理可知A1E′∥平面ADC1，E与E′重合，即可得出结论．
解答：
证明：（1）∵直三棱柱ABC-A1B1C1中，CC1⊥平面ABC，
而AD?平面ABC，∴CC1⊥AD；
又AB=AC，D为BC中点，∴AD⊥BC，
又BC∩CC1=C，BC?平面BCC1B1，CC1?平面BCC1B1，
∴AD⊥平面BCC1B1，
∵AD?平面ADC1，
∴平面ADC1⊥平面BCC1B1．
（2）设点E′是B1C1的中点
由（1）得AD⊥BC，
∵在△ABC中，AB=AC，
∴D为BC边上的中点，
连接DE′，∵点E′是B1C1的中点，
∴在直三棱柱ABC-A1B1C1中，四边形B1BDE′为平行四边形，
∴B1B∥E′D，B1B=E′D，
又B1B∥A1A，B1B=A1A，
∴E′D∥A1A，E′D=A1A，
∴四边形A1ADE′为平行四边形．
∴A1E′∥AD，又A1E′?平面ADC1，AD?平面ADC1，
∴A1E′∥平面ADC1．
∵A1E∥平面ADC1，
∴E与E′重合，
∴E为线段B1C1的中点．
而AD?平面ABC，∴CC1⊥AD；
又AB=AC，D为BC中点，∴AD⊥BC，
又BC∩CC1=C，BC?平面BCC1B1，CC1?平面BCC1B1，
∴AD⊥平面BCC1B1，
∵AD?平面ADC1，
∴平面ADC1⊥平面BCC1B1．
（2）设点E′是B1C1的中点
由（1）得AD⊥BC，
∵在△ABC中，AB=AC，
∴D为BC边上的中点，
连接DE′，∵点E′是B1C1的中点，
∴在直三棱柱ABC-A1B1C1中，四边形B1BDE′为平行四边形，
∴B1B∥E′D，B1B=E′D，
又B1B∥A1A，B1B=A1A，
∴E′D∥A1A，E′D=A1A，
∴四边形A1ADE′为平行四边形．
∴A1E′∥AD，又A1E′?平面ADC1，AD?平面ADC1，
∴A1E′∥平面ADC1．
∵A1E∥平面ADC1，
∴E与E′重合，
∴E为线段B1C1的中点．
点评：本题考查了空间中的平面与平面垂直以及直线与平面平行的问题，应熟练地掌握空间中的平行与垂直关系，来解答此类题目．
练习册系列答案
相关题目