题目内容
已知数列{an}满足a1=312,且3an+1=an(n∈N*,n≥1)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记数列bn=|log3an|,且数列{bn}的前n项和为Tn,求T30;
(Ⅲ)在(Ⅱ)的前提下,问从第几项开始数列{bn}中的连续20项之和等于102?
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记数列bn=|log3an|,且数列{bn}的前n项和为Tn,求T30;
(Ⅲ)在(Ⅱ)的前提下,问从第几项开始数列{bn}中的连续20项之和等于102?
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件求出q=
,由此能求出数列{an}的通项公式.
(Ⅱ)由an=313-n,知bn=|13-n|,由此能求出T30的值.
(Ⅲ)bn=|13-n|,记数列{bn}从第k项开始的连续20项和为Tk=bk+bk+1+…+bk+19,由此能求出结果.
| 1 |
| 3 |
(Ⅱ)由an=313-n,知bn=|13-n|,由此能求出T30的值.
(Ⅲ)bn=|13-n|,记数列{bn}从第k项开始的连续20项和为Tk=bk+bk+1+…+bk+19,由此能求出结果.
解答:
(本小题14分)
解:(Ⅰ)∵数列{an}满足a1=312,且3an+1=an,∴q=
,
∴an=312×(
)n-1=313-n.…(4分)
(Ⅱ)∵an=313-n,
∴bn=|13-n|,
∴T30=12+11+…+1+0+1+…+17
=
(1+12)+
(1+17)=231.…(8分)
(Ⅲ)bn=|13-n|,
记数列{bn}从第k项开始的连续20项和
为Tk=bk+bk+1+…+bk+19,
若k≥13,则Tk≥0+1+2+…+19=190>102,…(10分)
∴k<13,
∴Tk=bk+bk+1+…+b12+b13+b14+…+bk+19,
∴Tk=(13-k)+(12-k)+…+1+0+1+…+(k+6)
∴k2-7k+112=102,解得k=2或k=5.
∴从第2项或第5项开始数列{bn}中的连续20项之和等于102.…(14分)
解:(Ⅰ)∵数列{an}满足a1=312,且3an+1=an,∴q=
| 1 |
| 3 |
∴an=312×(
| 1 |
| 3 |
(Ⅱ)∵an=313-n,
∴bn=|13-n|,
∴T30=12+11+…+1+0+1+…+17
=
| 12 |
| 2 |
| 17 |
| 2 |
(Ⅲ)bn=|13-n|,
记数列{bn}从第k项开始的连续20项和
为Tk=bk+bk+1+…+bk+19,
若k≥13,则Tk≥0+1+2+…+19=190>102,…(10分)
∴k<13,
∴Tk=bk+bk+1+…+b12+b13+b14+…+bk+19,
∴Tk=(13-k)+(12-k)+…+1+0+1+…+(k+6)
|
∴k2-7k+112=102,解得k=2或k=5.
∴从第2项或第5项开始数列{bn}中的连续20项之和等于102.…(14分)
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法及其应用,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
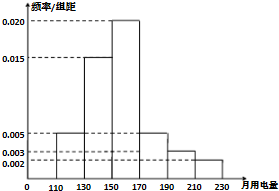 2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.
2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.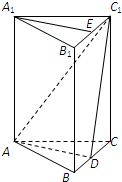 如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.