Question

设函数f(x)＝ln(1＋x)，g(x)＝xf′(x)，x≥0，其中f′(x)是f(x)的导函数．

(1)令g₁(x)＝g(x)，g_n＋1(x)＝g(g_n(x))，n∈N^*，求g_n(x)的表达式；

(2)若f(x)≥ag(x)恒成立，求实数a的取值范围．

Answer 1

解　由题设得，g(x)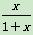＝(x≥0)．

(1)由已知得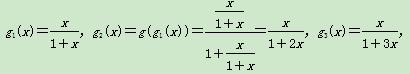，…，可得g_n(x)＝.

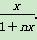下面用数学归纳法证明．

①当n＝1时，g₁(x)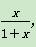＝，结论成立．

②假设n＝k时结论成立，

即g_k(x)＝.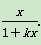

那么，当n＝k＋1时，g_k＋1(x)＝g(g_k(x))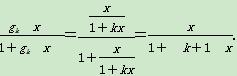＝即结论成立．

由①②可知，结论对n∈N^*成立．

(2)已知f(x)≥ag(x)恒成立，

即ln(1＋x)≥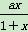恒成立．

设φ(x)＝ln(1＋x)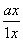－(x≥0)，

即，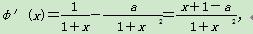

当a≤1时，φ′(x)≥0(仅当x＝0，a＝1时等号成立)，

∴φ(x)在[0，＋∞)上单调递增，又φ(0)＝0，

∴φ(x)≥0在[0，＋∞)上恒成立，

∴a≤1时，ln(1＋x)≥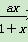恒成立(仅当x＝0时等号成立)．

当a>1时，对x∈(0，a－1]有φ′(x)<0，

∴φ(x)在(0，a－1]上单调递减，

∴φ(a－1)<φ(0)＝0.

即a>1时，存在x>0，使φ(x)<0，故知ln(1＋x)≥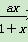不恒成立，

综上可知，a的取值范围是(－∞，1]．