题目内容
用数学归纳法证明：12＋32＋52＋…＋(2n－1)2＝
n(4n2－1)．
证明 (1)当n＝1时，左边＝12＝1，
右边＝×1×(4－1)＝1，等式成立．
(2)假设当n＝k(k∈N*)时等式成立，即12＋32＋52＋…＋(2k－1)2＝k(4k2－1)．
则当n＝k＋1时，12＋32＋52＋…＋(2k－1)2＋(2k＋1)2
＝k(4k2－1)＋(2k＋1)2＝k(4k2－1)＋4k2＋4k＋1
＝k[4(k＋1)2－1]－k·4(2k＋1)＋4k2＋4k＋1
＝k[4(k＋1)2－1]＋(12k2＋12k＋3－8k2－4k)
＝k[4(k＋1)2－1]＋[4(k＋1)2－1]
＝(k＋1)[4(k＋1)2－1]．
即当n＝k＋1时等式也成立．
由(1)，(2)可知，对一切n∈N*，等式都成立．
练习册系列答案
相关题目
图象上存在不同的三点到原点的距离构成等比数列，则以下不可能成为公比的数是( )
B.
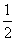
D.
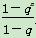，判断{an}是否为等比数列，并证明你的结论．
的解集是________．