题目内容
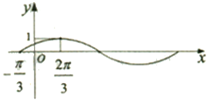 已知函数f(x)=sin(ωx+φ)(其中ω>0,φ∈(-
已知函数f(x)=sin(ωx+φ)(其中ω>0,φ∈(-| π |
| 2 |
| π |
| 2 |
(1)求ω、φ的值;
(2)设x∈(-
| π |
| 3 |
| π |
| 2 |
考点:y=Asin(ωx+φ)中参数的物理意义
专题:三角函数的图像与性质
分析:(1)首先,根据图象,得到周期,利用周期公式,确定ω=
,然后,将点(-
,0)代人函数解析式,求解得到该函数的解析式;
(2)根据x∈(-
,
),确定(
x+
)∈(0,
),然后,确定该函数的值域.
| 1 |
| 2 |
| π |
| 3 |
(2)根据x∈(-
| π |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 12 |
解答:
解:(1)根据题意,
=
-(-
)=π,
∴T=4π,
∴
=4π,
∴ω=
.
∴函数f(x)=sin(
x+φ),
把(-
,0)代人,得
sin(-
+φ)=0,且φ∈(-
,
)
∴φ=
,
综上,ω=
,φ=
,
(2)根据(1)得
f(x)=sin(
x+
),
∵x∈(-
,
),
∴(
x+
)∈(0,
),
∴sin(
x+
)∈(0,
).
∴函数f(x)的值域(0,
).
| T |
| 4 |
| 2π |
| 3 |
| π |
| 3 |
∴T=4π,
∴
| 2π |
| ω |
∴ω=
| 1 |
| 2 |
∴函数f(x)=sin(
| 1 |
| 2 |
把(-
| π |
| 3 |
sin(-
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
∴φ=
| π |
| 6 |
综上,ω=
| 1 |
| 2 |
| π |
| 6 |
(2)根据(1)得
f(x)=sin(
| 1 |
| 2 |
| π |
| 6 |
∵x∈(-
| π |
| 3 |
| π |
| 2 |
∴(
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 12 |
∴sin(
| 1 |
| 2 |
| π |
| 6 |
| ||||
| 4 |
∴函数f(x)的值域(0,
| ||||
| 4 |
点评:本题重点考查了三角函数的图象与性质,属于中档题.

练习册系列答案
相关题目