题目内容
甲、乙两地相距s千米,汽车从甲地匀速行驶到乙地,速度不超过60千米/小时,已知汽车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本与速度v(千米/小时)的平方成正比,已知速度为50千米/小时时每小时可变成本是100元;每小时固定成本为a元.
(1)把全程运输成本y(元)表示为速度v(千米/小时)的函数并标明定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
(1)把全程运输成本y(元)表示为速度v(千米/小时)的函数并标明定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
考点:基本不等式在最值问题中的应用
专题:导数的综合应用
分析:(1)由题意,总的运输成本y=每小时的运输成本×时间,而每小时的成本包括固定成本和可变成本,可变成本与速度的平方成正比,先利用待定系数法求出正比例系数,然后再用速度结合路程把时间表示出来,则全程的运输成本即可用速度v表示出来;
(2)由第一问得到了y关于速度v的函数,先利用导数研究其单调性,因为含有参数,所以要进行讨论,讨论的依据就是极值点(增间区间的分界点)与函数定义域的关系,一般分成极值点在区间内,区间左、区间右几种情况讨论.
(2)由第一问得到了y关于速度v的函数,先利用导数研究其单调性,因为含有参数,所以要进行讨论,讨论的依据就是极值点(增间区间的分界点)与函数定义域的关系,一般分成极值点在区间内,区间左、区间右几种情况讨论.
解答:
解(1)设可变成本=kv2,由已知得100=k•502,∴k=
,
∴可变成本=
v2,全程所用的时间为
,
∴全程运输成本为y=(a+
v2 )
=s(
+
),
所求函数及其定义域为y=s(
+
),v∈(0,60].
(2)∵y′=s(
-
)=
s=
s,v∈(0,60]
令y′=0得v=-5
(舍)或v=5
由题意:s,a,v均为正数,
∴当5
<60即0<a<144时,
y=s(
+
)在(0,5
]上单减,在[5
,60]上单增
所以当v=5
时,全程运输成本y最小.
(或用均值不等式:当5
<60即a<144时,y=s(
+
)≥2s
,当且仅当
=
,即v=5
时等号成立)
当5
≥60即a≥144时,
当v∈(0,60]时,y′<0,y=s(
+
)在(0,60]上单减,
∴此时当v=60时,全程运输成本y取最小值
综上,当0<a<144时,行驶速度v=5
千米/小时时全程成本最小,
∴当a≥144时,行驶速度v=60千米/小时时全程成本最小.
| 1 |
| 25 |
∴可变成本=
| 1 |
| 25 |
| s |
| v |
∴全程运输成本为y=(a+
| 1 |
| 25 |
| s |
| v |
| a |
| v |
| v |
| 25 |
所求函数及其定义域为y=s(
| a |
| v |
| v |
| 25 |
(2)∵y′=s(
| 1 |
| 25 |
| a |
| v2 |
| v2-25a |
| 25v2 |
(v+5
| ||||
| 25v2 |
令y′=0得v=-5
| a |
| a |
由题意:s,a,v均为正数,
∴当5
| a |
y=s(
| a |
| v |
| v |
| 25 |
| a |
| a |
所以当v=5
| a |
(或用均值不等式:当5
| a |
| a |
| v |
| v |
| 25 |
|
| a |
| v |
| v |
| 25 |
| a |
当5
| a |
当v∈(0,60]时,y′<0,y=s(
| a |
| v |
| v |
| 25 |
∴此时当v=60时,全程运输成本y取最小值
综上,当0<a<144时,行驶速度v=5
| a |
∴当a≥144时,行驶速度v=60千米/小时时全程成本最小.
点评:这是一道典型的利用导数研究其最值的应用题,一般遵循审题、设、列、解、答几大步,关键是审题过程,先要明确已知与所求,再找寻已知与所求的等量或不等关系,构造方程、函数、或者不等式;本题是一个函数应用题,需要求其最值,常采用导数方法先研究其在定义域内的单调性,然后再求最值;当然根据函数式的特征,也可以用基本不等式求最值,但要注意使用条件,即“一正、二定、三相等”.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
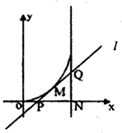 函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P、Q,点N(1,0),设△PQN的面积为S=g(t).
函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P、Q,点N(1,0),设△PQN的面积为S=g(t).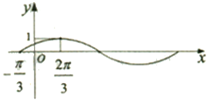 已知函数f(x)=sin(ωx+φ)(其中ω>0,φ∈(-
已知函数f(x)=sin(ωx+φ)(其中ω>0,φ∈(- 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF