题目内容

已知f（2x+1）=5x+3，则f（x）=
 
．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：用换元法，设2x+1=t，求出x，f（t）；即得f（x）．
解答： 解：设2x+1=t，t∈R，
∴x=
t-1
2
；
f（t）=5×
t-1
2
+3=
5t
2
+
1
2
；
∴f（x）=
5
2
x+
1
2
．
故答案为：
5
2
x+
1
2
．
点评：本题考查了求函数解析式的问题，解题时应根据题意，用换元法解答，是基础题．
练习册系列答案
相关题目
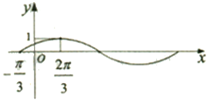已知扇形的周长为30，当它的半径R和圆心角α各取何值时，扇形的面积S最大？并求出扇形面积的最大值．
已知函数f（x）=sin（ωx+φ）（其中ω＞0，φ∈（-
π
2
，
π
2
））的部分图象如图所示．
（1）求ω、φ的值；
（2）设x∈（-
π
3
，
π
2
），求函数f（x）的值域．
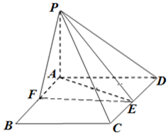如图，P-AD-C是直二面角，四边形ABCD为菱形，且∠BAD=120°，AB=2，PA⊥AD，E是CD的中点，设PC与平面ABCD所成的角为45°．
（1）求证：CD⊥平面PAE；
（2）试问在线段AB（不包括端点）上是否存在一点F，使得二面角A-PF-E的大小为45°？若存在，请求出AF的长，若不存在，请说明理由．
已知定义域为[0，1]的函数f（x）同时满足以下三个条件：
①对任意的x∈[0，1]，总有f（x）≥0；
②f（1）=1；
③当x1，x2∈[0，1]，且x1+x2∈[0，1]时，f（x1+x2）≥f（x1）+f（x2）成立．称这样的函数为“友谊函数”．
请解答下列各题：
（1）已知f（x）为“友谊函数”，求f（0）的值；
（2）函数g（x）=2x-1在区间[0，1]上是否为“友谊函数”？请给出理由；
（3）已知f（x）为“友谊函数”，假定存在x0∈[0，1]，使得f（x0）∈[0，1]，且f[f（x0）]=x0，求证：f（x0）=x0．
函数y=sin2x+2cosx-3的最大值是
 
．
已知-1，a1，a2，8成等差数列，-1，b1，b2，b3，-4成等比数列，那么
a1a2
b2
的值为
 
．
用反证法证明命题“如果x＜y，那么x3＜y3”时，假设的内容应该是
 
．
已知集合A={x|-1≤x≤1}，B={x|x≥a}，若A⊆B，则a的取值范围为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网