题目内容
在相距2km的A、B两点处测量目标点C，若∠CAB=75°，∠CBA=60°，则B、C两点之间的距离为（ ）
A、(
| ||
B、(
| ||
C、
| ||
D、2(
|
考点：解三角形的实际应用
专题：计算题,解三角形
分析：由题意，∠ACB=45°，则由正弦定理可得BC=
，即可得出结论．
| 2sin75° |
| sin45° |
解答：
解：由题意，∠ACB=45°，则
由正弦定理可得BC=
=
+1（km），
故选：B．
由正弦定理可得BC=
| 2sin75° |
| sin45° |
| 3 |
故选：B．
点评：本题考查解三角形的实际应用，考查学生的计算能力，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
在植物活动前为保证树苗的质量，林管部门会对树苗进行检测．先从甲、乙两种树苗中各抽测了10株树苗的高度，量出的高度（单位：厘米）制作成茎叶图如下，甲，乙两种树苗的平均高度分别记为| x |
| y |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式ax2-（a+2）x+2≥0（a＜0）的解集为（ ）
A、[
| ||
B、[1，
| ||
C、(-∞，
| ||
D、(-∞，1]∪[
|
函数f（x）=2sin（
-x）是（ ）
| π |
| 2 |
| A、最小正周期为2π的奇函数 |
| B、最小正周期为2π的偶函数 |
| C、最小正周期为π的奇函数 |
| D、最小正周期为4π的偶函数 |
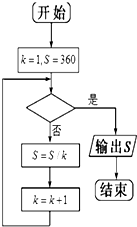执行如图所示的程序框图，运行的结果为S=3，那么判断框中应填入的关于k的判断条件是（ ）| A、k＞6？ | B、k＜6？ |
| C、k＞5？ | D、k＜5？ |