题目内容
11．已知函数$f（x）=\left\{\begin{array}{l}m{log_{2017}}x+3sinx，x＞0\\{log_{2017}}（-x）+nsinx，x＜0\end{array}\right.$为偶函数，则m-n=（ ）| A． | 4 | B． | 2 | C． | -2 | D． | -4 |
分析 根据题意，设x＞0，则有（-x）＜0，由函数f（x）的解析式可得f（x）=mlog2017x+3sinx以及f（-x）=log2017[-（-x）]+nsin（-x）=log2017x-nsinx，结合函数的奇偶性可得mlog2017x+3sinx=log2017x-nsinx，分析可得m、n的值，计算可得m-n的值．
解答 解：根据题意，设x＞0，（-x）＜0，
又由$f（x）=\left\{\begin{array}{l}m{log_{2017}}x+3sinx，x＞0\\{log_{2017}}（-x）+nsinx，x＜0\end{array}\right.$，
则f（x）=mlog2017x+3sinx，
则f（-x）=log2017[-（-x）]+nsin（-x）=log2017x-nsinx，
又由函数f（x）为偶函数，则有f（-x）=f（x），
即mlog2017x+3sinx=log2017x-nsinx，
则有m=1，n=-3；
则m-n=1-（-3）=4；
故选：A．
点评 本题考查函数奇偶性的性质，涉及分段函数的应用，关键是理解函数奇偶性的定义．
练习册系列答案
阅读快车系列答案
相关题目
1．已知Rt△ABC中，AB=3，AC=1，$∠A=\frac{π}{2}$，以B，C为焦点的双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）经过点A，且与AB边交于点D，若$\frac{{|{AD}|}}{{|{BD}|}}$的值为（ ）
| A． | $\frac{7}{2}$ | B． | 3 | C． | $\frac{9}{2}$ | D． | 4 |
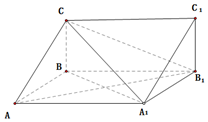如图，三棱柱ABC-A1B1C1中，四边形AA1BB1是菱形，∠BB1A1=$\frac{π}{3}，{C_1}{B_1}⊥面A{A_1}B{B_1}$，二面角C-A1B1-B为$\frac{π}{6}$，CB=1．