题目内容
3.已知实数x,y满足不等式组$\left\{\begin{array}{l}y-x≤2\\ x+y≥4\\ 3x-y≤5\end{array}\right.$,若目标函数z=y-mx取得最大值时有唯一的最优解(1,3),则实数m的取值范围是m>1.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,得到直线y=mx+z斜率的变化,从而求出m的取值范围.
解答 解:作出不等式组对应的平面区域如图,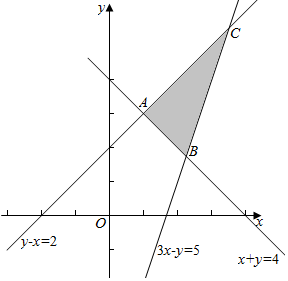
由z=y-mx,得y=mx+z,即直线的截距最大,z也最大,
若m=0,此时y=z,不满足条件;
若m>0,目标函数y=mx+z的斜率k=m>0,要使目标函数z=y-mx取得最大值时有唯一的最优解(1,3),
则直线y=mx+z的斜率m>1
若m<0,目标函数y=mx+z的斜率k=m<0,不满足题意.
综上,m>1.
故答案为:m>1.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.注意要对m进行分类讨论,是中档题.

练习册系列答案
相关题目
11.已知函数$f(x)=\left\{\begin{array}{l}m{log_{2017}}x+3sinx,x>0\\{log_{2017}}(-x)+nsinx,x<0\end{array}\right.$为偶函数,则m-n=( )
| A. | 4 | B. | 2 | C. | -2 | D. | -4 |
8.设数列{an}为等差数列,Sn为其前n项和,若S1≤13,S4≥10,S5≤15,则a4的最大值为( )
| A. | 3 | B. | 4 | C. | -7 | D. | -5 |
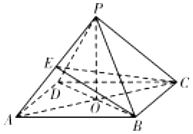 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=3,PA=$\sqrt{11}$,AC∩BD=O.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=3,PA=$\sqrt{11}$,AC∩BD=O.