题目内容
20.设等差数列{an}的公差d≠0,a1=2d,若ak是a1与a2k+7的等比中项,则k=( )| A. | 2 | B. | 3 | C. | 5 | D. | 8 |
分析 利用等差数列通项公式列出方程组,由此能求出k.
解答 解:∵等差数列{an}的公差d≠0,a1=2d,
ak是a1与a2k+7的等比中项,
∴$[{a}_{1}+(k-1)d]^{2}$=a1•[a1+(2k+6)d],且a1=2d,
解得k=5或k=-3(舍).
故选:C.
点评 本题考查等差数列的项数k的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知函数$f(x)=\left\{\begin{array}{l}m{log_{2017}}x+3sinx,x>0\\{log_{2017}}(-x)+nsinx,x<0\end{array}\right.$为偶函数,则m-n=( )
| A. | 4 | B. | 2 | C. | -2 | D. | -4 |
8.设数列{an}为等差数列,Sn为其前n项和,若S1≤13,S4≥10,S5≤15,则a4的最大值为( )
| A. | 3 | B. | 4 | C. | -7 | D. | -5 |
9.命题“?n∈N,f(n)∉N且f(n)≤n”的否定形式是( )
| A. | ?n∈N,f(n)∈N且f(n)>n | B. | ?n0∈N,f(n0)∈N且f(n0)>n0 | ||
| C. | ?n∈N,f(n)∈N或f(n)>n | D. | ?n0∈N,f(n0)∈N或f(n0)>n0 |
10.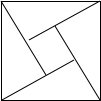 在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
 在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )| A. | 1-$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{4-\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
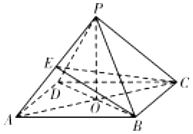 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=3,PA=$\sqrt{11}$,AC∩BD=O.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=3,PA=$\sqrt{11}$,AC∩BD=O.