��Ŀ����
6�������ĸ�����Բ���ߵ�����������A��BΪ�������㣬kΪ���㳣����$|\overrightarrow{PA}|+|\overrightarrow{PB}|=k$����P�Ĺ켣Ϊ��Բ��
���趨ԲC��һ����A��Բ�Ķ���AB��OΪ����ԭ�㣬��$\overrightarrow{OP}=\frac{1}{2}��\overrightarrow{OA}+\overrightarrow{OB}��$����P�Ĺ켣ΪԲ��
�۷���ln2x-lnx-2=0�������ɷֱ���Ϊ��Բ��˫���ߵ������ʣ�
��˫����$\frac{y^2}{9}-\frac{x^2}{25}=1$����Բ$\frac{x^2}{35}+{y^2}=1$����ͬ�Ľ��㣮
��������������Ϊ�ڢۣ�д���������������ţ�
���� �������⣬���η���4�����⣬���ڢ١�����Բ�Ķ�������ɵâٴ����ڢڡ������ɵ�P��AB�е㣬��ϴ������������ɵâ���ȷ�����ڢۡ��������ln2x-lnx-2=0�������������ɵ������Ĵ�С�ɵâ���ȷ�����ڢܡ�������Բ��˫���ߵĽ���λ�ü��ɵâܲ���ȷ���ۺϼ��ɵô𰸣�
��� �⣺�������⣬���η���4�����⣺
���ڢ١�������P�Ĺ켣Ϊ��Բ��������k��|AB|���ʢٴ���
���ڢڡ���$\overrightarrow{OP}=\frac{1}{2}��\overrightarrow{OA}+\overrightarrow{OB}��$����P��AB�е㣬����CPA=90�㣬����P�Ĺ켣����CAΪֱ����Բ���ʢ���ȷ��
���ڢۡ�����ln2x-lnx-2=0�������ֱ�Ϊx=e2��$\frac{1}{e}$����$\frac{1}{e}��1��{e^2}��1$���ʢ���ȷ��
���ڢܡ�˫���߽�����y���ϣ���Բ�Ľ�����x���ϣ��ʢܲ���ȷ
�ʴ�Ϊ���ڢۣ�
���� ���⿼�鳣��Բ���ߵĶ����Լ������ʣ��ؼ�������������Բ��˫���ߡ������ߵĵض��壮

��ϰ��ϵ�д�
 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�
�����Ŀ
16����֪������C��y2=4x�Ľ���ΪF������F����б��Ϊ$\frac{��}{3}$��ֱ����������C���߽��ڵ�B�����߶�FB�ij�Ϊ��������
| A�� | 10 | B�� | 6 | C�� | 8 | D�� | 4 |
1����ֱ��y=x�ϴ��ڵ㣨x��y������Լ������$\left\{\begin{array}{l}x+y-4��0\\ x-2y-3��0\\ x��m\end{array}\right.$����ʵ��m�����ֵΪ��������
| A�� | -1 | B�� | 1 | C�� | $\frac{3}{2}$ | D�� | 2 |
11����֪����$f��x��=\left\{\begin{array}{l}m{log_{2017}}x+3sinx��x��0\\{log_{2017}}��-x��+nsinx��x��0\end{array}\right.$Ϊż��������m-n=��������
| A�� | 4 | B�� | 2 | C�� | -2 | D�� | -4 |
16��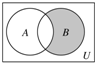 ��֪ȫ��U=Z��A={x��Z|x2-x-2��0}��B={-1��0��1��2}����ͼ����Ӱ��������ʾ�ļ��ϵ��ڣ�������
��֪ȫ��U=Z��A={x��Z|x2-x-2��0}��B={-1��0��1��2}����ͼ����Ӱ��������ʾ�ļ��ϵ��ڣ�������
 ��֪ȫ��U=Z��A={x��Z|x2-x-2��0}��B={-1��0��1��2}����ͼ����Ӱ��������ʾ�ļ��ϵ��ڣ�������
��֪ȫ��U=Z��A={x��Z|x2-x-2��0}��B={-1��0��1��2}����ͼ����Ӱ��������ʾ�ļ��ϵ��ڣ�������| A�� | {-1��2} | B�� | {-1��0} | C�� | {0��1} | D�� | {1��2} |