题目内容
16.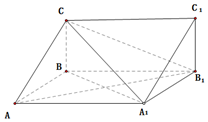 如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.
如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.(Ⅰ)求证:平面ACB1⊥平面CBA1;
(Ⅱ)求二面角A-A1C-B的余弦值.
分析 (Ⅰ)证明CB⊥AB1,AB1⊥A1B,推出AB1⊥面A1BC,然后证明平面ACB1⊥平面CBA1
(Ⅱ)说明∠CDB为二面角C-A1B1-B的平面角,过AB1,A1B交点O作OE⊥A1C,垂足为E,连AE,说明∠AEO为二面角A-A1C-B的平面角然后求解即可.
解答 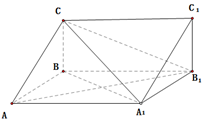 (Ⅰ)证明:在三棱柱ABC-A1B1C1中,由C1B1⊥面AA1BB1
(Ⅰ)证明:在三棱柱ABC-A1B1C1中,由C1B1⊥面AA1BB1
得CB⊥面AA1BB1,则CB⊥AB1,…(2分)
又AA1BB1是菱形,得AB1⊥A1B,而CB∩A1B=B,
则AB1⊥面A1BC,…(4分)
故平面ACB1⊥平面CBA1.…(5分)
(Ⅱ)由题意得△A1B1B为正三角形,
取A1B1得中点为D,连CD,BD,
则BD⊥A1B1,又CB⊥A1B1
易得CD⊥A1B1,则∠CDB为二面角C-A1B1-B的平面角,
因BC=1,∠CDB=$\frac{π}{6}$,所以$BD=\sqrt{3}$,
所以A1B1=BB1=A1B=2
过AB1,A1B交点O作OE⊥A1C,垂足为E,连AE
则∠AEO为二面角A-A1C-B的平面角,…(9分)
又$OE=\frac{{\sqrt{5}}}{5},AO=\sqrt{3}$得$AE=\frac{{4\sqrt{5}}}{5}$
所以$cos∠AEO=\frac{1}{4}$…(12分)
另:建系用向量法相应给分.
点评 本题考查二面角的平面角的求法,直线与平面垂直的判定定理的应用,考查空间想象能力逻辑推理能力以及计算能力.

练习册系列答案
相关题目
6.在区间[0,2]内随机取出两个数,则这两个数的平方和在区间[0,2]内的概率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{8}$ |
11.已知函数$f(x)=\left\{\begin{array}{l}m{log_{2017}}x+3sinx,x>0\\{log_{2017}}(-x)+nsinx,x<0\end{array}\right.$为偶函数,则m-n=( )
| A. | 4 | B. | 2 | C. | -2 | D. | -4 |
1.已知P是△ABC所在平面内一点,$\overrightarrow{PB}+\overrightarrow{PC}+4\overrightarrow{PA}=\overrightarrow 0$,现在△ABC内任取一点,则该点落在△PBC内的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
8.设数列{an}为等差数列,Sn为其前n项和,若S1≤13,S4≥10,S5≤15,则a4的最大值为( )
| A. | 3 | B. | 4 | C. | -7 | D. | -5 |