题目内容
1.已知函数f(x)=$\frac{x}{lnx}$-ax+b在点(e,f(e))处的切线方程为y=-ax+2e.(Ⅰ)求实数b的值;
(Ⅱ)若存在x∈[e,e2],满足f(x)≤$\frac{1}{4}$+e,求实数a的取值范围.
分析 (Ⅰ)求导,利用导数的几何意义,直线的点斜式方程,即可求得实数b的值;
(Ⅱ)则a≥$\frac{1}{lnx}$-$\frac{1}{4x}$在[e,e2]上有解,构造辅助函数,求导,利用导数与函数单调性的关系,求得h(x)的取值.
解答 解:(Ⅰ)f(x)=$\frac{x}{lnx}$-ax+b,x∈(0,1)∪(1,+∞),
求导,f′(x)=$\frac{lnx-1}{l{n}^{2}x}$-a,
则函数f(x)在点(e,f(e))处切线方程y-(e-ex+b)=-a(x-e),
即y=-ax+e+b,
由函数f(x)在(e,f(e))处的切线方程为y=-ax+2e,比较可得b=e,
实数b的值e;
(Ⅱ)由f(x)≤$\frac{1}{4}$+e,即$\frac{x}{lnx}$-ax+e≤$\frac{1}{4}$+e,
则a≥$\frac{1}{lnx}$-$\frac{1}{4x}$在[e,e2],上有解,
设h(x)=$\frac{1}{lnx}$-$\frac{1}{4x}$,x∈[e,e2],
求导h′(x)=$\frac{1}{4{x}^{2}}$-$\frac{1}{xl{n}^{2}x}$=$\frac{l{n}^{2}x-4x}{4{x}^{2}l{n}^{2}x}$=$\frac{(lnx+2\sqrt{x})(lnx-2\sqrt{x})}{4{x}^{2}l{n}^{2}x}$,
令p(x)=lnx-2$\sqrt{x}$,
∴x在[e,e2]时,p′(x)=$\frac{1}{x}$-$\frac{1}{\sqrt{x}}$=$\frac{1-\sqrt{x}}{x}$<0,
则函数p(x)在[e,e2]上单调递减,
∴p(x)<p(e)=lne-2$\sqrt{e}$<0,
则h′(x)<0,及h(x)在区间[e,e2]单调递减,
h(x)≥h(e2)=$\frac{1}{ln{e}^{2}}$-$\frac{1}{4{e}^{2}}$=$\frac{1}{2}$-$\frac{1}{4{e}^{2}}$,
∴实数a的取值范围[$\frac{1}{2}$-$\frac{1}{4{e}^{2}}$,+∞].
点评 本题考查导数的综合应用,导数的几何意义,利用导数求函数的切线方程,利用导数求函数的单调性及最值,考查计算能力,属于中档题.

 高中必刷题系列答案
高中必刷题系列答案| A. | 4 | B. | 2 | C. | -2 | D. | -4 |
| A. | ?n∈N,f(n)∈N且f(n)>n | B. | ?n0∈N,f(n0)∈N且f(n0)>n0 | ||
| C. | ?n∈N,f(n)∈N或f(n)>n | D. | ?n0∈N,f(n0)∈N或f(n0)>n0 |
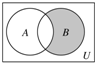 已知全集U=Z,A={x∈Z|x2-x-2<0},B={-1,0,1,2},则图中阴影部分所表示的集合等于( )
已知全集U=Z,A={x∈Z|x2-x-2<0},B={-1,0,1,2},则图中阴影部分所表示的集合等于( )| A. | {-1,2} | B. | {-1,0} | C. | {0,1} | D. | {1,2} |
 在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )| A. | 1-$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{4-\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
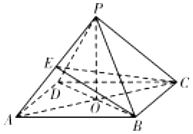 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=3,PA=$\sqrt{11}$,AC∩BD=O.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=3,PA=$\sqrt{11}$,AC∩BD=O.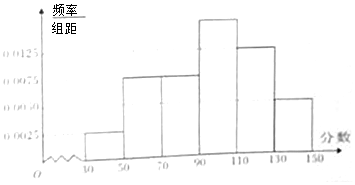 某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图:
某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图: