题目内容
1.已知Rt△ABC中,AB=3,AC=1,$∠A=\frac{π}{2}$,以B,C为焦点的双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)经过点A,且与AB边交于点D,若$\frac{{|{AD}|}}{{|{BD}|}}$的值为( )| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{9}{2}$ | D. | 4 |
分析 运用双曲线定义,可得2a=3-1=2,设|BD|=t,运用双曲线的定义,求得|DC|,|AD|,再由直角三角形的勾股定理,解方程可得t,进而得到|AD|,即可得到答案.
解答 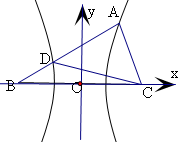 解:如图,双曲线的焦点为B(-c,0),C(c,0),
解:如图,双曲线的焦点为B(-c,0),C(c,0),
由双曲线的定义可得|AB|-|AC|=2a=3-1=2,
设|BD|=t,由双曲线的定义可得|DC|=2a+|BD|=2a+t=2+t,
又|AD|=3-t,
在直角三角形ACD中,|AC|2+|AD|2=|CD|2,
即为1+(3-t)2=(2+t)2,
解得t=0.6,|AD|=3-0.6=2.4.
则$\frac{{|{AD}|}}{{|{BD}|}}$的值为$\frac{2.4}{0.6}$=4.
故选:D.
点评 本题考查双曲线的定义的运用,考查直角三角形的勾股定理,以及化简整理的运算能力,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
9.已知集合A={3,2,-1,-2},m∈A,n∈A方程mx2+ny2=1表示的图形记为“W”,则W表示双曲线的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{8}$ |
6.在区间[0,2]内随机取出两个数,则这两个数的平方和在区间[0,2]内的概率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{8}$ |