题目内容
 如图,在正三棱柱ABC-A1B1C1中,点D为棱AB的中点,BC=1,AA1=
如图,在正三棱柱ABC-A1B1C1中,点D为棱AB的中点,BC=1,AA1=| 3 |
(1)求证:BC1∥平面A1DC;
(2)求三棱锥D-A1B1C 的体积.
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)连接AC1,交A1C于点O,连结OD,由已知得OD∥BC1,由此能证明BC1∥平面A1DC.
(2)由已知得AB⊥CD,从而CD⊥平面ABB1A1,进而CD⊥平面DB1A1,由此能求出三棱锥D-A1B1C 的体积.
(2)由已知得AB⊥CD,从而CD⊥平面ABB1A1,进而CD⊥平面DB1A1,由此能求出三棱锥D-A1B1C 的体积.
解答:
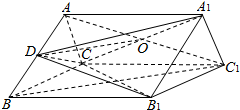 (1)证明:连接AC1,交A1C于点O,连结OD,
(1)证明:连接AC1,交A1C于点O,连结OD,
∵ACC1A1是平行四边形,
∴O为AC1中点,
∵D为AB的中点,
∴OD∥BC1,OD=
BC1,BC1?平面A1CD,OD?平面A1CD,
∴BC1∥平面A1DC.
(2)解:正△ABC中,
∵D为AB的中点,
∴AB⊥CD,
又∵平面ABC⊥平面ABB1A1,
∴CD⊥平面ABB1A1,
∴CD⊥平面DB1A1,
∵CD=
,S△A1B1D=
,
∴VD-A1B1C= C-A1B1D=
CD•S△A1B1D=
×
×
=
.
 (1)证明:连接AC1,交A1C于点O,连结OD,
(1)证明:连接AC1,交A1C于点O,连结OD,∵ACC1A1是平行四边形,
∴O为AC1中点,
∵D为AB的中点,
∴OD∥BC1,OD=
| 1 |
| 2 |
∴BC1∥平面A1DC.
(2)解:正△ABC中,
∵D为AB的中点,
∴AB⊥CD,
又∵平面ABC⊥平面ABB1A1,
∴CD⊥平面ABB1A1,
∴CD⊥平面DB1A1,
∵CD=
| ||
| 2 |
| ||
| 2 |
∴VD-A1B1C= C-A1B1D=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
点评:本题考查直线与平面平行的证明,考查三棱锥的体积的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
已知命题p:“任意x∈R时,都有x2-x+
>0”;命题q:“存在x∈R,使sinx+cosx=
成立”.则下列判断正确的是( )
| 1 |
| 4 |
| 2 |
| A、命题q为假命题 |
| B、命题P为真命题 |
| C、p∧q为真命题 |
| D、p∨q是真命题 |
已知圆的方程式x2+y2=36,记过点P(1,2)的最长弦和最短弦分别为AB、CD,则直线AB、CD的斜率之和等于( )
| A、-1 | ||
B、
| ||
| C、1 | ||
D、-
|
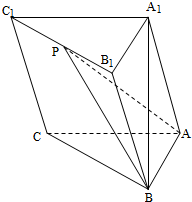 如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC. 如图,棱长为2的正方体ABCD-A1B1C1D1中,E为棱C1D1上的动点,F为棱BC的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,E为棱C1D1上的动点,F为棱BC的中点.