题目内容
已知圆的方程式x2+y2=36，记过点P（1，2）的最长弦和最短弦分别为AB、CD，则直线AB、CD的斜率之和等于（ ）
| A、-1 | ||
B、
| ||
| C、1 | ||
D、-
|
考点：直线与圆相交的性质
专题：直线与圆
分析：根据过圆心的弦最长，以P为中点的弦最短，进行求解即可．
解答：
解：圆心坐标为O（O，O），
当过点P（1，2）的最长弦AB过圆心O时，AB最长此时AB的斜率k=
=2，
过点P（1，2）的弦以P为中点时，此时弦CD最短，此时满足CD⊥AB．
则AB的斜率k=-
，
则直线AB、CD的斜率之和等于-
+2=
，
故选：B．
当过点P（1，2）的最长弦AB过圆心O时，AB最长此时AB的斜率k=
| 2 |
| 1 |
过点P（1，2）的弦以P为中点时，此时弦CD最短，此时满足CD⊥AB．
则AB的斜率k=-
| 1 |
| 2 |
则直线AB、CD的斜率之和等于-
| 1 |
| 2 |
| 3 |
| 2 |
故选：B．
点评：本题主要考查直线和圆的位置关系的应用，要求理解最长弦和最短弦的位置．
练习册系列答案
相关题目
已知命题p：对任意x1，x2∈R，（f（x2）-f（x1））（x2-x1）≥0，则“非p”是（ ）
| A、存在x1，x2∈R，使（f（x2）-f（x1））（x2-x1）＜0 |
| B、对任意x1，x2∈R，都有（f（x2）-f（x1））（x2-x1）≤0 |
| C、存在x1，x2∈R，使（f（x2）-f（x1））（x2-x1）≤0 |
| D、对任意x1，x2∈R，都有（f（x2）-f（x1））（x2-x1）＜0 |
如图，在正三棱柱ABC-A1B1C1中，点D为棱AB的中点，BC=1，AA1=
在梯形ABCD中，AB∥CD，如果分别以下列各选项所给的内容作为已知条件，那么其中不能确定BD长度的选项是（ ）| A、AC=4，∠ABD=45°，∠ACD=30° | ||
B、AB=2，CD=2
| ||
C、AB=2，CD=2
| ||
D、CD=2
|
已知函数f（x）=lnx+
+ax，x∈（0，+∞）（a为实常数）．若f（x）在[2，+∞）上是单调函数，则a的取值范围是（ ）
| 1 |
| x |
A、（-∞，-
| ||
B、（-∞，-
| ||
C、（-∞，0）∪[
| ||
D、（-∞，0）∪（
|
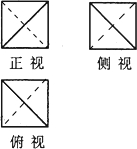正方体的四个顶点构成的几何体的三视图如图，若各视图均为边长为2的正方形，则这个几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，已知AB是半圆O的直径，AB=8，M，N，P是将半圆圆周四等分的三个分点，从A，B，M，N，P这5个点中任取3个点，则这3个点组成直角三角形的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|